Advanced Placement (AP): Construct the probability distribution of the random variable Y.

Advanced Placement (AP) : asked on giovney

06.01.2021

Construct the probability distribution of the random variable Y.

Get Answer

Faq

Mathematics

Let x denote the sum of two distinct numbers selected randomly from the set of numbers StartSet 1 comma 2 comma 3 comma 4 comma 5 EndSet . {1, 2, 3, 4, 5}. Construct the probability distribution for the random variable x.

Step-by-step answer

P Answered by PhD

Step-by-step explanation:

Given:

The set of numbers {1, 2, 3, 4, 5}

Affter that, we find the sum um of two distinct numbers selected randomly from the set above;

1+2 =31+3=41+4=51+5=62+3=52+4=62+5=73+4=73+5=84+5 = 9

Therefore, we have the following number: 3,4,5,6,5,6,7,7,8,9

so we have x = {3,4,5,6,5,6,7,7,8,9 }

now we find P(x) of each number, we have n(S) = 10

x 3456789

P(x) 1/101/101/102/102/102/101/10

Hope it will find you well.

Mathematics

Step-by-step answer

P Answered by PhD

Step-by-step explanation:

Given:

The set of numbers {1, 2, 3, 4, 5}

Affter that, we find the sum um of two distinct numbers selected randomly from the set above;

1+2 =31+3=41+4=51+5=62+3=52+4=62+5=73+4=73+5=84+5 = 9

Therefore, we have the following number: 3,4,5,6,5,6,7,7,8,9

so we have x = {3,4,5,6,5,6,7,7,8,9 }

now we find P(x) of each number, we have n(S) = 10

x 3456789

P(x) 1/101/101/102/102/102/101/10

Hope it will find you well.

Mathematics

In the game of roulette, a wheel consists of 38 slots numbered 0, 00, 1, 2,..., 36. To play the game, a metal ball is spun around the wheel and is allowed to fall into one of the numbered slots. If the number of the slot the ball falls into matches the number you selected, you win $35; otherwise you lose $1.A)Construct a probability distribution for the random variable X, the winnings of each spin. X P(X) 35 .0263 -1 .9737 (b) Determine the mean and standard deviation of the random variable X. Round your results to the nearest penny.

Step-by-step answer

P Answered by PhD

a) Probability distribution of the winnings is given in the table below

X ||| P(X)

35 | 0.0263

-1 | 0.9737

b) Mean = -$0.0532 = -$0.0532 to the nearest penny; that is, 5 pennies.

Standard deviation = $5.76 = 576 pennies to the nearest penny.

Step-by-step explanation:

To construct the probability distribution, we first define the random variable X which represents the winnings of each spin

X can take on value of $35; that is, a win of $35 when the number of the slot the ball falls into matches the number you selected

And a value of -$1; that is, a loss of $1 if the number of the slot the ball falls into does not match the number you selected.

Note that there are 38 slots. And one can only select 1 slot at a time.

So, the probability that one wins when the slot that one selects is the right slot = (1/38) = 0.0263

Probability of losing = 1 - 0.0263 = 0.9737

So, the probability distribution is now given as

X ||| P(X)

35 | 0.0263

-1 | 0.9737

b) Mean and Standard deviation of the random variable X

Mean = Expected value.

Expected value = E(X) = Σ xᵢpᵢ

where xᵢ = each variable

pᵢ = probability of each variable

E(X) = (35)(0.0263) + (-1)(0.9737)

= 0.9205 - 0.9737 = -$0.0532 = -$0.05 to the nearest penny; thanks 5 pennies to the nearest penny.

Standard deviation = √(variance)

Variance = Var(X) = Σx²p − μ²

where μ = E(X) = -0.0532

Σx²p = (35²)(0.0263) + (-1)²(0.9737)

= 32.2175 + 0.9737 = 33.1912

Var(X) = 33.1912 - (-0.0532)² = 33.18836976

Standard deviation = √(variance)

= √(33.18836976) = $5.76; that is, 576 pennies.

Hope this Helps!!!

Mathematics

Suppose the following data represent the ratings (on a scale from 1 to 5) for a certain smart phone game, with 1 representing a poor rating. The discrete probability distribution for the random variable x is given below: Star Frequency 1 2140 2 2853 3 4734 4 4880 5 10,715 Required: Construct a discrete probability distribution for the random variable X

Step-by-step answer

P Answered by Specialist

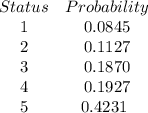
$\begin{array}{cc}{Status} & {Probability} & {1} & {0.0845} & {2} & {0.1127} & {3} & {0.1870} & {4} & {0.1927}& {5} & {0.4231} \ \end{array}$

Step-by-step explanation:

Given

The above table

Required

The discrete probability distribution

The probability of each is calculated as:

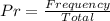
$Pr = \frac{Frequency}{Total}$

Where:

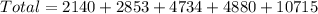
Total = 2140+ 2853 + 4734 + 4880 + 10715

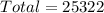
Total = 25322

So, we have:

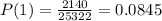
$P(1) = \frac{2140}{25322} = 0.0845$

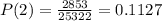
$P(2) = \frac{2853}{25322} = 0.1127$

$P(3) = \frac{4734}{25322} = 0.1870$

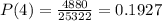
$P(4) = \frac{4880}{25322} = 0.1927$

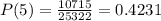
$P(5) = \frac{10715}{25322} = 0.4231$

So, the discrete probability distribution is:

$\begin{array}{cc}{Status} & {Probability} & {1} & {0.0845} & {2} & {0.1127} & {3} & {0.1870} & {4} & {0.1927}& {5} & {0.4231} \ \end{array}$

Mathematics

Step-by-step answer

P Answered by Master

$\begin{array}{cc}{Status} & {Probability} & {1} & {0.0845} & {2} & {0.1127} & {3} & {0.1870} & {4} & {0.1927}& {5} & {0.4231} \ \end{array}$

Step-by-step explanation:

Given

The above table

Required

The discrete probability distribution

The probability of each is calculated as:

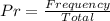
$Pr = \frac{Frequency}{Total}$

Where:

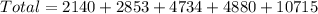
Total = 2140+ 2853 + 4734 + 4880 + 10715

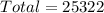
Total = 25322

So, we have:

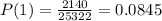
$P(1) = \frac{2140}{25322} = 0.0845$

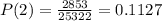
$P(2) = \frac{2853}{25322} = 0.1127$

$P(3) = \frac{4734}{25322} = 0.1870$

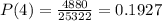
$P(4) = \frac{4880}{25322} = 0.1927$

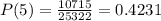
$P(5) = \frac{10715}{25322} = 0.4231$

So, the discrete probability distribution is:

$\begin{array}{cc}{Status} & {Probability} & {1} & {0.0845} & {2} & {0.1127} & {3} & {0.1870} & {4} & {0.1927}& {5} & {0.4231} \ \end{array}$

Mathematics

Construct the discrete probability distribution for the random variable described. Express the probabilities as simplified fractions. The number of heads in 4 tosses of a coin.

Step-by-step answer

P Answered by PhD

Discrete probability distribution

X 0 1 2 3 4

P(X=x) 1/16 4/16 6/16 4/16 1/16

Step-by-step explanation:

Discrete Random variable:-

A random variable X which can take only a finite number of discrete values

In an interval domain is called a discrete random variable. In other words

a real valued function defined on a discrete sample space is called a

Discrete Random variable.

For example : X(s) = { s: s = 0, 1, 2} The random variable X is a discrete Random variable.

Given the number of heads in 4 tosses of a coin

The total number of possible events is n(S) = 2^4 = 16

Discrete distribution:-

The random variable X is a discrete Random variable.

X(x) = { x: x = 0, 1, 2,3,4}

Here x=0 means → no heads that is the possible outcomes are only one

n(E) = {T,T,T,T} = 1

P(X=0) = 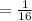$=\frac{1}{16}$

Here x=1 means → one head and three tails that is the possible outcomes are '4'

n(E) ={( HTTT),(THTT),(TTHT),(TTTH)

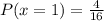
$P(x=1) = \frac{4}{16}$

Here x=2means → TWO head and TWO tails that is the possible outcomes are '6'

n(E) = {( HHTT),(THHT),(TTHH),(HTTH),(THTH),(HTHT)

n(E) = 6

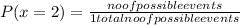
$P(x=2) = \frac{no of possible events}{1total no of possible events}$

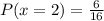
$P(x=2) = \frac{6}{16}$

Here x=3means → three head and one tails that is the possible outcomes are '4'

n(E) = { HHHT,HTHH,HHTH,THHH} =3

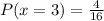
$P(x=3) = \frac{4}{16}$

Here x=4 means → FOUR heads that is the possible outcomes are only one

n(E) = {HHHH} = 1

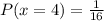
$P(x=4) = \frac{1}{16}$

Final -

Discrete probability distribution

X 0 1 2 3 4

P(X=x) 1/16 4/16 6/16 4/16 1/16

Mathematics

Construct the discrete probability distribution for the random variable described. Express the probabilities as simplified fractions. The number of tails in 5 tosses of a coin.

Step-by-step answer

P Answered by Specialist

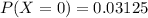
P(X = 0) = 0.03125

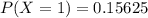
P(X = 1) = 0.15625

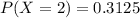
P(X = 2) = 0.3125

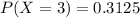
P(X = 3) = 0.3125

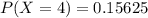
P(X = 4) = 0.15625

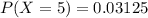
P(X = 5) = 0.03125

Step-by-step explanation:

For each toss, there are only two possible outcomes. Either it is tails, or it is not. The probability of a toss resulting in tails is independent of any other toss, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

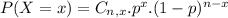
$P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}$

In which 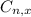$C_{n,x}$ is the number of different combinations of x objects from a set of n elements, given by the following formula.

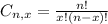
$C_{n,x} = \frac{n!}{x!(n-x)!}$

And p is the probability of X happening.

Fair coin:

Equally as likely to be heads or tails, so 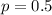p = 0.5

5 tosses:

This means that 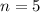n = 5

Probability distribution:

Probability of each outcome, so:

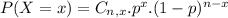
$P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}$

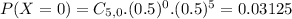
$P(X = 0) = C_{5,0}.(0.5)^{0}.(0.5)^{5} = 0.03125$

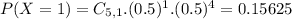
$P(X = 1) = C_{5,1}.(0.5)^{1}.(0.5)^{4} = 0.15625$

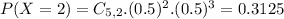
$P(X = 2) = C_{5,2}.(0.5)^{2}.(0.5)^{3} = 0.3125$

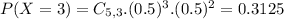
$P(X = 3) = C_{5,3}.(0.5)^{3}.(0.5)^{2} = 0.3125$

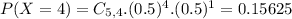
$P(X = 4) = C_{5,4}.(0.5)^{4}.(0.5)^{1} = 0.15625$

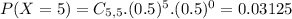
$P(X = 5) = C_{5,5}.(0.5)^{5}.(0.5)^{0} = 0.03125$

Mathematics

Construct the discrete probability distribution for the random variable described. Express the probabilities as simplified fractions. The number of heads in 4 tosses of a coin.

Step-by-step answer

P Answered by PhD

Discrete probability distribution

X 0 1 2 3 4

P(X=x) 1/16 4/16 6/16 4/16 1/16

Step-by-step explanation:

Discrete Random variable:-

A random variable X which can take only a finite number of discrete values

In an interval domain is called a discrete random variable. In other words

a real valued function defined on a discrete sample space is called a

Discrete Random variable.

For example : X(s) = { s: s = 0, 1, 2} The random variable X is a discrete Random variable.

Given the number of heads in 4 tosses of a coin

The total number of possible events is n(S) = 2^4 = 16

Discrete distribution:-

The random variable X is a discrete Random variable.

X(x) = { x: x = 0, 1, 2,3,4}

Here x=0 means → no heads that is the possible outcomes are only one

n(E) = {T,T,T,T} = 1

P(X=0) = 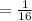$=\frac{1}{16}$

Here x=1 means → one head and three tails that is the possible outcomes are '4'

n(E) ={( HTTT),(THTT),(TTHT),(TTTH)

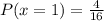
$P(x=1) = \frac{4}{16}$

Here x=2means → TWO head and TWO tails that is the possible outcomes are '6'

n(E) = {( HHTT),(THHT),(TTHH),(HTTH),(THTH),(HTHT)

n(E) = 6

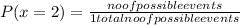
$P(x=2) = \frac{no of possible events}{1total no of possible events}$

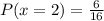
$P(x=2) = \frac{6}{16}$

Here x=3means → three head and one tails that is the possible outcomes are '4'

n(E) = { HHHT,HTHH,HHTH,THHH} =3

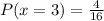
$P(x=3) = \frac{4}{16}$

Here x=4 means → FOUR heads that is the possible outcomes are only one

n(E) = {HHHH} = 1

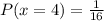
$P(x=4) = \frac{1}{16}$

Final -

Discrete probability distribution

X 0 1 2 3 4

P(X=x) 1/16 4/16 6/16 4/16 1/16

Mathematics

Construct the discrete probability distribution for the random variable described. Express the probabilities as simplified fractions. The number of tails in 4 tosses of a coin.

Step-by-step answer

P Answered by PhD

The discrete probability distribution table for the outcome of tails obtainable from 4 coin tosses :

Number of tails __ 0 __1 __ 2 __ 3 __ 4 Probability ____ 1/16_1/4__3/8 _1/4 _1/16

Sample space for 4 coin tosess:

{HHHH, HHHT, HHHT, HHTT, HTHH, HTHT, HTHT, HTTT, THHH, THHT, THHT, THTT, TTHH, TTHT, TTHT, TTTT}

Recall :

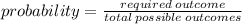
$probability = \frac{required \: outcome}{total \: possible \: outcomes}$

Possible Number of tails are 0, 1, 2, 3 and 4

For 0 tail :

P(0T) = 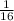$\frac{1}{16}$

For 1 tail :

P(1T) = 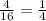$\frac{4}{16} = \frac{1}{4}$

For 2 tails :

P(2T) = 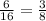$\frac{6}{16} = \frac{3}{8}$

For 3 tails :

P(3T) = 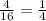$\frac{4}{16} = \frac{1}{4}$

For 4 tails :

P(4T) = 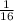$\frac{1}{16}$

Therefore, the discrete probability distribution table is displayed thus :

Number of tails __ 0 __1 __ 2 __ 3 __ 4 Probability ____ 1/16 _1/4 _3/8 _1/4 _1/16

Learn more :link

Mathematics

For questions, 1-2, determine whether experiment is a binomial experiment. if it is, identify a success, specify the values of n, p, and q, and list the possible values of the random variable x. if it is not a binomial experiment, explain why. 1. a survey found that 49% of u.s. households own a dedicated game console. eight u.s. households are randomly selected. the random variable represents the number of u.s. households that own a dedicated game console. you draw five cards, one at a time, from a standard deck. you do not replace a card once

Step-by-step answer

P Answered by Master

Part 1

X="number of U.S. households that own a dedicated game console"

Is a binomial experiment we an event defined with the associated probability and we have specific trials.

Let X the random variable of interest, on this case we now that:

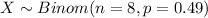
$X \sim Binom(n=8, p=0.49)$

Y= "number of cards that are hearts."

Thats not a binomial experiment since the probability for each trial changes since we are doing the experiment without replacment

Part 2

a) 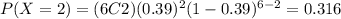$P(X=2)=(6C2)(0.39)^2 (1-0.39)^{6-2}=0.316$

b) 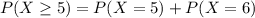$P(X \geq 5) = P(X=5)+P(X=6)$

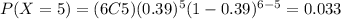
$P(X=5)=(6C5)(0.39)^5 (1-0.39)^{6-5}=0.033$

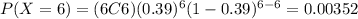
$P(X=6)=(6C6)(0.39)^6 (1-0.39)^{6-6}=0.00352$

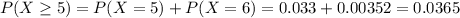
$P(X \geq 5) = P(X=5)+P(X=6)=0.033+0.00352=0.0365$

Part 3

Let X the random variable of interest, on this case we now that:

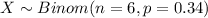
$X \sim Binom(n=6, p=0.34)$

The probability mass function for the Binomial distribution is given as:

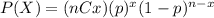
$P(X)=(nCx)(p)^x (1-p)^{n-x}$

Part 4

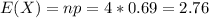
E(X)=np=4*0.69=2.76

The variance 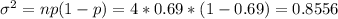$\sigma^2 = np(1-p) = 4*0.69*(1-0.69) =0.8556$

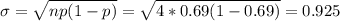
$\sigma=\sqrt{np(1-p)}=\sqrt{4*0.69(1-0.69)}=0.925$

Unusual outcomes would be considered values above or below 2 deviations from the mean for example 2.76-(2*0.925) =0.91 or 2.76+2(0.925)=4.61[/tex]. X=0 and X=4 would be considered as unusual values.

Step-by-step explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Part 1

X="number of U.S. households that own a dedicated game console"

Is a binomial experiment we an event defined with the associated probability and we have specific trials.

Let X the random variable of interest, on this case we now that:

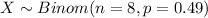
$X \sim Binom(n=8, p=0.49)$

Y= "number of cards that are hearts."

Thats not a binomial experiment since the probability for each trial changes since we are doing the experiment without replacment

Part 2

Let X the random variable of interest, on this case we now that:

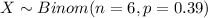
$X \sim Binom(n=6, p=0.39)$

The probability mass function for the Binomial distribution is given as:

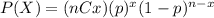
$P(X)=(nCx)(p)^x (1-p)^{n-x}$

Where (nCx) means combinatory and it's given by this formula:

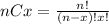
$nCx=\frac{n!}{(n-x)! x!}$

And we want to find this probability:

a) 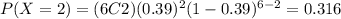$P(X=2)=(6C2)(0.39)^2 (1-0.39)^{6-2}=0.316$

b) 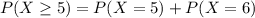$P(X \geq 5) = P(X=5)+P(X=6)$

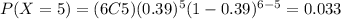
$P(X=5)=(6C5)(0.39)^5 (1-0.39)^{6-5}=0.033$

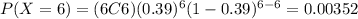
$P(X=6)=(6C6)(0.39)^6 (1-0.39)^{6-6}=0.00352$

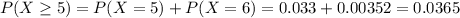
$P(X \geq 5) = P(X=5)+P(X=6)=0.033+0.00352=0.0365$

Part 3

Let X the random variable of interest, on this case we now that:

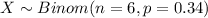
$X \sim Binom(n=6, p=0.34)$

The probability mass function for the Binomial distribution is given as:

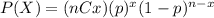
$P(X)=(nCx)(p)^x (1-p)^{n-x}$

Part 4

Let X the random variable of interest, on this case we now that:

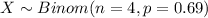
$X \sim Binom(n=4, p=0.69)$

The probability mass function for the Binomial distribution is given as:

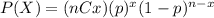
$P(X)=(nCx)(p)^x (1-p)^{n-x}$

The expected value is given by:

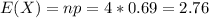
E(X)=np=4*0.69=2.76

The variance 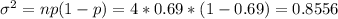$\sigma^2 = np(1-p) = 4*0.69*(1-0.69) =0.8556$

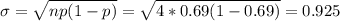
$\sigma=\sqrt{np(1-p)}=\sqrt{4*0.69(1-0.69)}=0.925$

Unusual outcomes would be considered values above or below 2 deviations from the mean for example 2.76-(2*0.925) =0.91 or 2.76+2(0.925)=4.61[/tex]. X=0 and X=4 would be considered as unusual values.

free Ask question

Today we have helped

323 students

just now

Mathematics

If the baseball radius is 1.4 inches what is the circumfrance in inches

m Answered by Master

1 minute ago

Chemistry

g The gas molecules in the internal combustion engine chamber are in a high state of random motion. When the molecules are expelled through an exhaust pipe in a more ordered state, what will their temperature be as their temperature in the chamber before being exhausted

p Answered by PhD

1 minute ago