 41
41 Vertex: (0, 0); Focus: (0, -10); Directrix: y = 10; Focal width: 10
2. C) y equals negative 1 divided by 8 x squared
3. D) x equals negative 1 divided by 32 y squared
4. C) x2 = -5.3y
5. C) Center: (0, 0); Vertices: (0, -15), (0, 15); Foci: (0, -12), (0, 12)
6. None from the choices, it should be
Center: (0, 0); Vertices: the point negative two square root two comma zero and the point 2 square root two comma zero; Foci: Ordered pair negative square root 6 comma zero and ordered pair square root 6 comma zero
7. B) A vertical ellipse is shown on the coordinate plane centered at the origin with vertices at the point zero comma seven and zero comma negative seven. The minor axis has endpoints at negative six comma zero and six comma zero.
8. D) x squared divided by 16 plus y squared divided by 25 equals 1
9. D) Vertices: (1, -1), (-11, -1); Foci: (-15, -1), (5, -1)
 41
41 Vertex: (0, 0); Focus: (0, -10); Directrix: y = 10; Focal width: 10
2. C) y equals negative 1 divided by 8 x squared
3. D) x equals negative 1 divided by 32 y squared
4. C) x2 = -5.3y
5. C) Center: (0, 0); Vertices: (0, -15), (0, 15); Foci: (0, -12), (0, 12)
6. None from the choices, it should be
Center: (0, 0); Vertices: the point negative two square root two comma zero and the point 2 square root two comma zero; Foci: Ordered pair negative square root 6 comma zero and ordered pair square root 6 comma zero
7. B) A vertical ellipse is shown on the coordinate plane centered at the origin with vertices at the point zero comma seven and zero comma negative seven. The minor axis has endpoints at negative six comma zero and six comma zero.
8. D) x squared divided by 16 plus y squared divided by 25 equals 1
9. D) Vertices: (1, -1), (-11, -1); Foci: (-15, -1), (5, -1)






















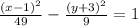





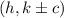
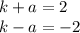



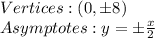
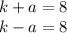


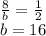 .
. 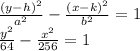
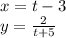


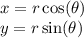
 .
.
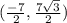

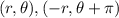


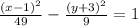





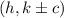
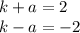



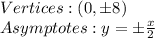
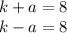


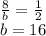 .
. 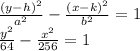
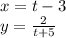


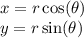
 .
.
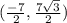

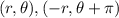


 29
29 1. It is shifted 2 units down.
The graph of 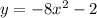 is shifted 2 units down with respect to the graph of
is shifted 2 units down with respect to the graph of 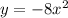 . We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
. We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
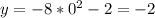
In the second function:
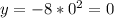
So, the first graph is shifted 2 units down.
2. 160.56 m
The path of the rocket is given by:
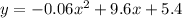
The problem asks us to find how far horizontally the rocket lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
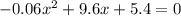
Using the formula,
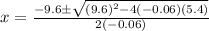
which has two solutions: 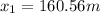 and
and 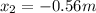 . The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
. The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
3. 27.43 m
The path of the rock is given by:
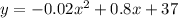
The problem asks us to find how far horizontally the rock lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
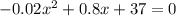
Using the formula,
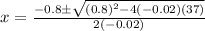
which has two solutions: 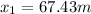 and
and 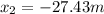 . In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
. In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
4. (-2, 16) and (1, -2)
The system is:
 (1)
(1)
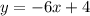 (2)
(2)
We can equalize the two equations:
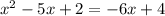
which becomes:
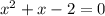
Solving it with the formula, we find two solutions: x=-2 and x=1. Substituting both into eq.(2):
x=-2 --> 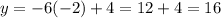
x=1 --> 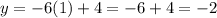
So, the solutions are (-2, 16) and (1, -2).
5. (-1, 1) and (7, 33)
The system is:
 (1)
(1)
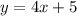 (2)
(2)
We can equalize the two equations:
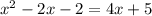
which becomes:
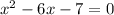
Solving it with the formula, we find two solutions: x=7 and x=-1. Substituting both into eq.(2):
x=7 --> 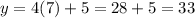
x=-1 --> 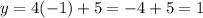
So, the solutions are (-1, 1) and (7, 33).
6. 2.30 seconds
The height of the object is given by:
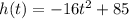
The time at which the object hits the ground is the time t at which the height becomes zero: h(t)=0, therefore
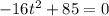
By solving it,
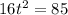
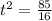
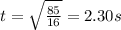
7. Reaches a maximum height of 19.25 feet after 0.88 seconds.
The height of the ball is given by
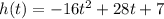
The vertical velocity of the ball is equal to the derivative of the height:
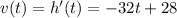
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
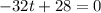
from which we find 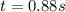
And by substituting these value into h(t), we find the maximum height:
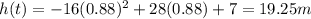
8. Reaches a maximum height of 372.25 feet after 4.63 seconds.
The height of the boulder is given by
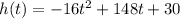
The vertical velocity of the boulder is equal to the derivative of the height:
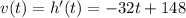
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
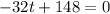
from which we find 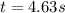
And by substituting these value into h(t), we find the maximum height:
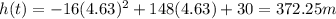
9. 12 m
Let's call x the length of the side of the original garden. The side of the new garden has length (x+3), so its area is
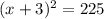
Solvign this equation, we find
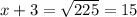
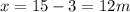
10. 225/4
In fact, if we write 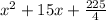 , we see this is equivalent to the perfect square:
, we see this is equivalent to the perfect square:
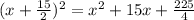
11. -11.56, 1.56
The equation is:
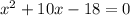
By using the formula:
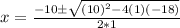
which has two solutions: x=-11.56 and 1.56.
12. -10.35, 1.35
The equation is:
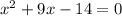
By using the formula:
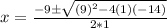
which has two solutions: x=-10.35 and 1.35.
 29
29 1. It is shifted 2 units down.
The graph of 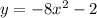 is shifted 2 units down with respect to the graph of
is shifted 2 units down with respect to the graph of 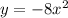 . We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
. We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
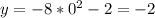
In the second function:
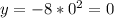
So, the first graph is shifted 2 units down.
2. 160.56 m
The path of the rocket is given by:
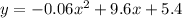
The problem asks us to find how far horizontally the rocket lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
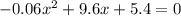
Using the formula,
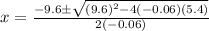
which has two solutions: 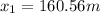 and
and 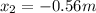 . The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
. The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
3. 27.43 m
The path of the rock is given by:
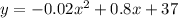
The problem asks us to find how far horizontally the rock lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
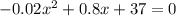
Using the formula,
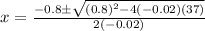
which has two solutions: 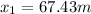 and
and 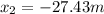 . In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
. In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
4. (-2, 16) and (1, -2)
The system is:
 (1)
(1)
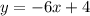 (2)
(2)
We can equalize the two equations:
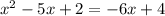
which becomes:
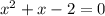
Solving it with the formula, we find two solutions: x=-2 and x=1. Substituting both into eq.(2):
x=-2 --> 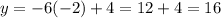
x=1 --> 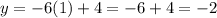
So, the solutions are (-2, 16) and (1, -2).
5. (-1, 1) and (7, 33)
The system is:
 (1)
(1)
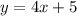 (2)
(2)
We can equalize the two equations:
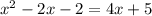
which becomes:
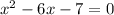
Solving it with the formula, we find two solutions: x=7 and x=-1. Substituting both into eq.(2):
x=7 --> 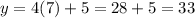
x=-1 --> 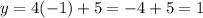
So, the solutions are (-1, 1) and (7, 33).
6. 2.30 seconds
The height of the object is given by:
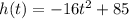
The time at which the object hits the ground is the time t at which the height becomes zero: h(t)=0, therefore
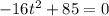
By solving it,
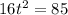
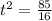
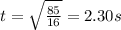
7. Reaches a maximum height of 19.25 feet after 0.88 seconds.
The height of the ball is given by
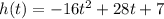
The vertical velocity of the ball is equal to the derivative of the height:
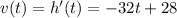
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
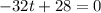
from which we find 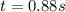
And by substituting these value into h(t), we find the maximum height:
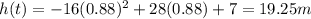
8. Reaches a maximum height of 372.25 feet after 4.63 seconds.
The height of the boulder is given by
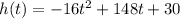
The vertical velocity of the boulder is equal to the derivative of the height:
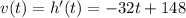
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
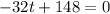
from which we find 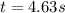
And by substituting these value into h(t), we find the maximum height:
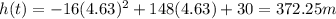
9. 12 m
Let's call x the length of the side of the original garden. The side of the new garden has length (x+3), so its area is
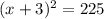
Solvign this equation, we find
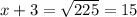
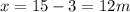
10. 225/4
In fact, if we write 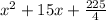 , we see this is equivalent to the perfect square:
, we see this is equivalent to the perfect square:
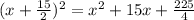
11. -11.56, 1.56
The equation is:
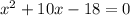
By using the formula:
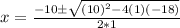
which has two solutions: x=-11.56 and 1.56.
12. -10.35, 1.35
The equation is:
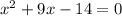
By using the formula:
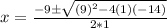
which has two solutions: x=-10.35 and 1.35.
 16
16 You have the first 2 here's most of the rest. Write the equation that models the height of the roller coaster. Start by writing the equation of the circle . (Recall that the general form of a circle with the center at the origin isx2+ y2 = r2. x^2+y^2=30^2, The radius is 30 ftx^2+y^2=900 Now solve this equation for y. Remember the roller coaster is above ground, so you are only interested in the positive root. y = √(900 -x^2) Graph the model of the roller coaster using the graphing calculator. Take a screenshot of your graph and paste the image below, or sketch a graph by hand. (Put this in you should be good ) y= root (900)-x^2 x^2+y^2=900 all your points should equal 30 and look like a semi circle, but on the top part of the top not the bottom. Write the equation you would need to solve to find the horizontal distance each beam is from the origin.(x=√30^2-25^2) Algebraically solve the equation you found in step 3. Round your answer to the nearest hundredth. 16.584.Explain where to place the two beams x= -16.58x=16.58 Graph the cable and the strut on the model of the roller coaster using the graphing calculator. Take a screenshot of your graph and paste the image below, or sketch a graph by hand 900= x^2 +y^2 y=root(900-x^2) y= ^2x +8 y= x-8 the intersection should be -10 and positive 10 enter those equation into your calculator. That's all I know so far
Step-by-step explanation:
 8
8 The car stops at a distance from the starting point because the portion shows a constant function away from the starting point.
Step-by-step explanation:
For this case, the first thing you should keep in mind is the following definition:
d = v * t
Where,
d: distance
v: speed
t: time
For the portion of the chart labeled J we have:
The time increases
The distance is the same
We have then that the speed is zero.
Therefore, the car is stopped at a distance far from the starting point.
The car stops at a distance from the starting point because the portion shows a constant function away from the starting point.

It will provide an instant answer!
