Explanation:
Enter number of terms (1-10000): 1000
Estimated value: 3.14059
Enter number of terms (1-10000): 1
Estimated value: 4
Enter number of terms (1-10000): 10000
Estimated value: 3.14149
Enter number of terms (1-10000): 100000
Error!!
Code (modify count statements)
#include <bits/stdc++,h>
using namespace std;
#define Id long double
Id pi(int n){
Id sum=0:
int sign=1;
for(int i=0;i<n;i++){
Id num= sign*1.00/(2*i+1);
sign*=-1;
sum+=num;
}
return 4*sum;
}
int main(){
int n;
count<<"Welcome\n";
count<<"Enter number of terms(1-1000):";
cin>>n;
while(n!=99){
if(n>10000 or n<1)
count<<"Error!!\n";
else{
count<<"Estimated value;"<<pi(n)<<endl;
count<<endl<<endl;
}
count<<"Enter number of terms(1-10000):";
cin>>n;
}
}
Explanation:
Enter number of terms (1-10000): 1000
Estimated value: 3.14059
Enter number of terms (1-10000): 1
Estimated value: 4
Enter number of terms (1-10000): 10000
Estimated value: 3.14149
Enter number of terms (1-10000): 100000
Error!!
Code (modify count statements)
#include <bits/stdc++,h>
using namespace std;
#define Id long double
Id pi(int n){
Id sum=0:
int sign=1;
for(int i=0;i<n;i++){
Id num= sign*1.00/(2*i+1);
sign*=-1;
sum+=num;
}
return 4*sum;
}
int main(){
int n;
count<<"Welcome\n";
count<<"Enter number of terms(1-1000):";
cin>>n;
while(n!=99){
if(n>10000 or n<1)
count<<"Error!!\n";
else{
count<<"Estimated value;"<<pi(n)<<endl;
count<<endl<<endl;
}
count<<"Enter number of terms(1-10000):";
cin>>n;
}
}
 2
2 Correct option is (d): Neither X nor Y can be well-approximated by a normal random variable.
Step-by-step explanation:
The sample size of males having color-blindness is, n (X) = 20.
The sample size of females having color-blindness is, n (Y) = 40.
The proportion of males that suffer from color-blindness is, P (X) = 0.08.
The proportion of females that suffer from color-blindness is, P (Y) = 0.01.
Now both the random variables X and Y follows a Binomial distribution,
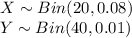
A normal distribution is used to approximate the binomial distribution if the sample is large, i.e n ≥ 30 and the probability of success is very close to 0.50.
Also if np ≥ 10 and n (1 - p) ≥ 10, the binomial distribution can be approximated by the normal distribution.
For the sample of men (X):
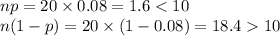
In this case neither n > 30 nor p is close to 0.50.
And np < 10.
Thus, the random variable X cannot be approximated by the normal distribution.
For the sample of men (Y):
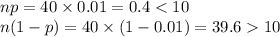
In this case n > 30 but p is not close to 0.50.
And np < 10.
Thus, the random variable Y cannot be approximated by the normal distribution.
Thus, both the random variables cannot be approximated by the normal distribution.
The correct option is (d).
(a) Approximately 68 % of women in this group have platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7.
(b) Approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.
Step-by-step explanation:
We are given that the blood platelet counts of a group of women have a bell-shaped distribution with a mean of 257.62 and a standard deviation of 62.1
Let X = the blood platelet counts of a group of women
So, X ~ Normal(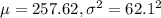 )
)
Now, the empirical rule states that;
68% of the data values lie within the 1 standard deviation of the mean.95% of the data values lie within the 2 standard deviations of the mean.99.7% of the data values lie within the 3 standard deviations of the mean.(a) The approximate percentage of women with platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7 is 68% according to the empirical rule.
(b) The approximate percentage of women with platelet counts between 71.3 and 443.9 is given by;
z-score of 443.9 = 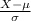
= 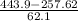 = 3
= 3
z-score of 71.3 = 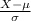
= 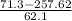 = -3
= -3
So, approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.
a) Approximately 99.7% of women in this group have platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4.
b) Approximately 68% of women in this group have platelet counts between 201.6 and 328.0.
Step-by-step explanation:
The Empirical Rule states that, for a normally distributed(bell shaped) random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean = 264.8
Standard deviation = 63.2
a. What is the approximate percentage of women with platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4?
By the Empirical Rule,
Approximately 99.7% of women in this group have platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4.
b. What is the approximate percentage of women with platelet counts between 201.6 and 328.0?
201.6 = 264.8 - 63.2
201.6 is one standard deviation below the mean
328 = 264.8 + 63.2
328 is one standard deviation above the mean
By the Empirical rule,
Approximately 68% of women in this group have platelet counts between 201.6 and 328.0.
(a) Approximately 68 % of women in this group have platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7.
(b) Approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.
Step-by-step explanation:
We are given that the blood platelet counts of a group of women have a bell-shaped distribution with a mean of 257.62 and a standard deviation of 62.1
Let X = the blood platelet counts of a group of women
So, X ~ Normal(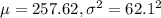 )
)
Now, the empirical rule states that;
68% of the data values lie within the 1 standard deviation of the mean.95% of the data values lie within the 2 standard deviations of the mean.99.7% of the data values lie within the 3 standard deviations of the mean.(a) The approximate percentage of women with platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7 is 68% according to the empirical rule.
(b) The approximate percentage of women with platelet counts between 71.3 and 443.9 is given by;
z-score of 443.9 = 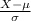
= 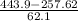 = 3
= 3
z-score of 71.3 = 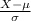
= 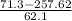 = -3
= -3
So, approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.
a) Approximately 99.7% of women in this group have platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4.
b) Approximately 68% of women in this group have platelet counts between 201.6 and 328.0.
Step-by-step explanation:
The Empirical Rule states that, for a normally distributed(bell shaped) random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean = 264.8
Standard deviation = 63.2
a. What is the approximate percentage of women with platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4?
By the Empirical Rule,
Approximately 99.7% of women in this group have platelet counts within 3 standard deviations of the mean, or between 75.2 and 454.4.
b. What is the approximate percentage of women with platelet counts between 201.6 and 328.0?
201.6 = 264.8 - 63.2
201.6 is one standard deviation below the mean
328 = 264.8 + 63.2
328 is one standard deviation above the mean
By the Empirical rule,
Approximately 68% of women in this group have platelet counts between 201.6 and 328.0.
 4
4 Given, Annapolis, Maryland has an approximate population of 36,000.
And Columbus, Ohio has an approximate population of 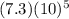 .
.
First we have to multiply 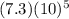 .
.
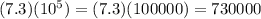
We can see the population of columbus is larger than population of Annapolis.
Now we will divide the population of Columbus by the population of Annapolis to find how much times the population of columbus is larger. We will get,
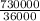 = 20.28 ( Approximately taken upto two decimal place)
= 20.28 ( Approximately taken upto two decimal place)
So it is more than 20 times.
We can say, The population of columbus is approximately 20 times larger than Annapolis.
We have got the required answer.
Option 3 is correct.
 4
4 Given, Annapolis, Maryland has an approximate population of 36,000.
And Columbus, Ohio has an approximate population of 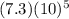 .
.
First we have to multiply 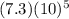 .
.
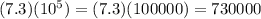
We can see the population of columbus is larger than population of Annapolis.
Now we will divide the population of Columbus by the population of Annapolis to find how much times the population of columbus is larger. We will get,
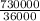 = 20.28 ( Approximately taken upto two decimal place)
= 20.28 ( Approximately taken upto two decimal place)
So it is more than 20 times.
We can say, The population of columbus is approximately 20 times larger than Annapolis.
We have got the required answer.
Option 3 is correct.
(a)20.65 lbs.
(b)1.88 lbs/month.
Step-by-step explanation:
The median weight of the boy can be approximated by the function:
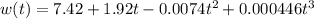
Where t is measured in months; and
w is measured in pounds.
(a)When the baby is 7 months
Approximate Weight,
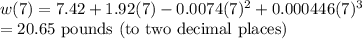
The approximate weight of the baby at age 7 months is 20.65 lbs.
(b) If 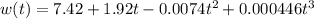
Rate of change, 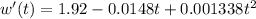
At t=7 months
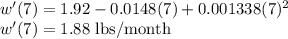
The rate of change for the baby's weight with respect to time at age 7 months is approximately 1.88 lbs/month.

It will provide an instant answer!
