 1
1 Step-by-step explanation:
{9, 14, 19, ...} so it looks like 5 is added to the previous term to get next
The recursive rule may be


The fith term is you find by writing the arithmetic sequence formula
 , where d is how much you add
, where d is how much you add
yet for the 5th term
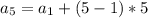
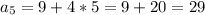
 1
1 Step-by-step explanation:
{9, 14, 19, ...} so it looks like 5 is added to the previous term to get next
The recursive rule may be


The fith term is you find by writing the arithmetic sequence formula
 , where d is how much you add
, where d is how much you add
yet for the 5th term
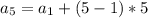
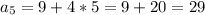
Hello,
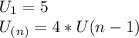

Step-by-step explanation:
Given

Required
An explicit rule for 
Where 
We have:

Calculate a2
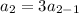
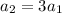
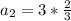

Calculate a3


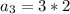

Calculate a4


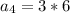
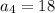
Calculate a5


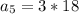

So:




The above sequence form a geometric sequence.
Calculate common ratio (r)




So, the explicit formula is:

 , so:
, so:

 , so:
, so:

Split:



The explicit rule is: 

Step-by-step explanation:
Given

Required
An explicit rule for 
Where 
We have:

Calculate a2
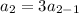
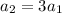
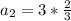

Calculate a3


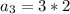

Calculate a4


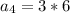
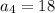
Calculate a5


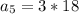

So:




The above sequence form a geometric sequence.
Calculate common ratio (r)




So, the explicit formula is:

 , so:
, so:

 , so:
, so:

Split:



The explicit rule is: 
ANSWER
See explanation
EXPLANATION
Question 1:
The third term of the arithmetic sequence is :
14=a+2d...(1)
The twelveth term is
59=a+11d...(2)
Subtract equation (1) from (2)
45=9d
This implies that
d=5
a=14-2(5)=4
The explicit rule is;



Recursive formula:
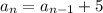
Question 2
The geometric sequence has the fourth term to be 2 and the common ratio to be r=⅓
This implies that,
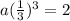
This implies that,


The explicit rule:

The recursive rule is

where,

ANSWER
See explanation
EXPLANATION
Question 1:
The third term of the arithmetic sequence is :
14=a+2d...(1)
The twelveth term is
59=a+11d...(2)
Subtract equation (1) from (2)
45=9d
This implies that
d=5
a=14-2(5)=4
The explicit rule is;



Recursive formula:
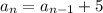
Question 2
The geometric sequence has the fourth term to be 2 and the common ratio to be r=⅓
This implies that,
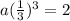
This implies that,


The explicit rule:

The recursive rule is

where,

 11
11  11
11  for
for 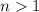
Step-by-step explanation:
Given
 -- First Term
-- First Term
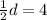 --- half common difference
--- half common difference
Required
Find the recursive rule
First, we calculate the common difference
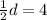
Multiply through by 2

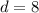
The second term of the sequence is:

The third term is:

So, we have:


Substitute f(1) for 3

Express 1 as 2 - 1

Substitute n for 2

Similarly:
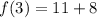
Substitute f(2) for 11

Express 2 as 3 - 1

Substitute n for 3

Hence, the recursive is:
 for
for 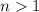

It will provide an instant answer!
