 4
4 =65 181/290
Step-by-step explanation:
The minimum cost is arrived to when ΔC/Δx is zero.
ΔC/Δx= 2.2x-638
We equate this to zero to get the minimum.
2.2x-638=0
2.2x=638
x=290
The cost for 290 engines is given by:
C(x)=1.1x²-638x+111,541
We replace the value of x above in this function.
=1.1(290)²-638(290)+111541
=19 031
Then 1 unit costs 19031/290
=65 181/290
$14,362
Step-by-step explanation:
The computation of the minimum unit cost is shown below:
Given that
0.6x^2 - 108x + 19,222
And as we know that the quadratic equation form is
ax^2 + bx + c
where
a = 0.6
b = -108
c = 19,222
Now for determining the minimal cost we applied the following formula which is
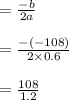
= 90
Now put these values to the above equation
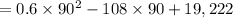
= 14,362
 5
5 Minimum Unit Cost = $14,362
Step-by-step explanation:
The standard form of a quadratic is given by:
ax^2 + bx + c
So for our function, we can say,
a = 0.6
b = -108
c = 19,222
We can find the vertex (x-coordinate where minimum value occurs) by the formula -b/2a
So,
-(-108)/2(0.6) = 108/1.2 = 90
Plugging this value into original function would give us the minimum (unit cost):
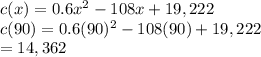
 4
4 =65 181/290
Step-by-step explanation:
The minimum cost is arrived to when ΔC/Δx is zero.
ΔC/Δx= 2.2x-638
We equate this to zero to get the minimum.
2.2x-638=0
2.2x=638
x=290
The cost for 290 engines is given by:
C(x)=1.1x²-638x+111,541
We replace the value of x above in this function.
=1.1(290)²-638(290)+111541
=19 031
Then 1 unit costs 19031/290
=65 181/290
The function is missing in the question. The function is 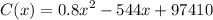
The answer is 4930
Step-by-step explanation:
Unit cost of a car is given as
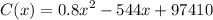
Cost will be minimum when
x = -(-544)/ 2 x 0.8
= 340
Therefore, minimum cost for unit car is
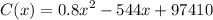
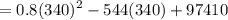
= 4930
 2
2 The minimum unit cost is $5257
Step-by-step explanation:
Minimization
Given a function c(x), the minimum value of c can be found by computing the first derivative. Equating the first derivative to zero will provide the critical points, or candidate point to maximize or minimize the function. The second derivative criterion will make clear which type of point was obtained.
The cost in dollars to produce x machines is
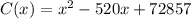
Find the first derivative
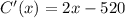
Equate to 0
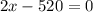
Solving:
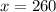
There must be produced 260 machines to minimize the cost. The minimum cost is
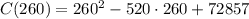
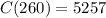
The minimum unit cost is $5257
 1
1 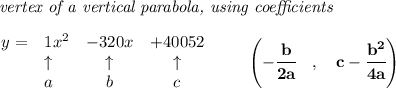
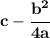
 1
1 The minimum unit cost is 5377
Step-by-step explanation:
Note that we have a cudratic function of negative principal coefficient.
The minimum value reached by this function is found in its vertex.
For a quadratic function of the form
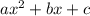
the x coordinate of the vertex is given by the following expression
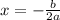
In this case the function is:
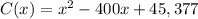
So:
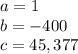
Then the x coordinate of the vertex is:
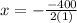
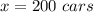
So the minimum unit cost is:
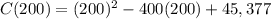
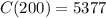
 5
5 1.The most cost-effective order quantity (assuming they take the most cost-effective discount, and use a fixed holding cost) is 182 units.
2. At the chosen level of quantity, discount, and using the fixed holding cost, the total annual cost for Bell computers to order, purchase, and hold the integrated chips is $1,585,898.
When holding costs are 10% of purchase price per unit,1.The most cost-effective order quantity (assuming they take the most cost-effective discount, and use a fixed holding cost) is 189 units.
2. At the chosen level of quantity, discount, and using the fixed holding cost, the total annual cost for Bell computers to order, purchase, and hold the integrated chips is $1,585,546.
When holding costs are $35 per unit,We follow these steps to arrive at the
1. We have
Ordering Costs per order $119
Holding Cost per unit $35
Demand per month 405 units
Demand per year is 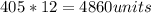
Since the most cost-effective order quantity is the Economic Order Quantity (EOQ), we compute the EOQ
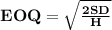
where
D is demand per year
S is the Ordering cost per order
H is the holding cost per unit
Substituting the values we get,
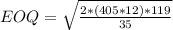
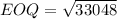
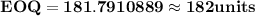
2. The annual costs of ordering, purchasing and holding the integrated chips is the sum of the cost of ordering, purchasing and holding the integrated chips.
Since the EOQ at 182 units falls in the second slab of Rich Blue Manufacturing, Bell computer can purchase chips at $325 per unit
Cost of purchasing the chips 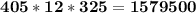
Number of orders to placed 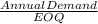
Number of orders to placed 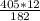
Number of orders to placed 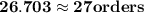
Cost of orders 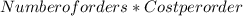
Cost of orders 
Holding Costs 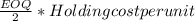
Holding Costs 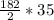
Holding Costs 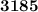
Total annual costs 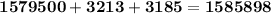
1. We need to calculate the EOQ, which holding cost at each purchase price
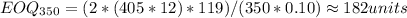
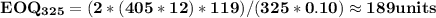
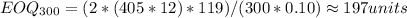
Since the EOQ lies between 100 and 199 units in all the three costs, Bell Computers can purchase the units only at $325 per unit, so its holding cost will be 10% of $325, which is $32.50 per unit.
2.2. The annual costs of ordering, purchasing and holding the integrated chips is the sum of the cost of ordering, purchasing and holding the integrated chips.
Since the EOQ at 189 units falls in the second slab of Rich Blue Manufacturing, Bell computer can purchase chips at $325 per unit
Cost of purchasing the chips 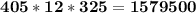
Number of orders to placed 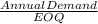
Number of orders to placed 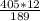
Number of orders to placed 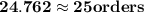
Cost of orders 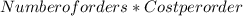
Cost of orders 
Holding Costs 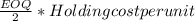
Holding Costs 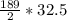
Holding Costs 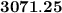
Total annual costs 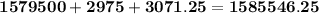
 5
5 1.The most cost-effective order quantity (assuming they take the most cost-effective discount, and use a fixed holding cost) is 182 units.
2. At the chosen level of quantity, discount, and using the fixed holding cost, the total annual cost for Bell computers to order, purchase, and hold the integrated chips is $1,585,898.
When holding costs are 10% of purchase price per unit,1.The most cost-effective order quantity (assuming they take the most cost-effective discount, and use a fixed holding cost) is 189 units.
2. At the chosen level of quantity, discount, and using the fixed holding cost, the total annual cost for Bell computers to order, purchase, and hold the integrated chips is $1,585,546.
When holding costs are $35 per unit,We follow these steps to arrive at the
1. We have
Ordering Costs per order $119
Holding Cost per unit $35
Demand per month 405 units
Demand per year is 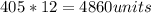
Since the most cost-effective order quantity is the Economic Order Quantity (EOQ), we compute the EOQ
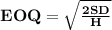
where
D is demand per year
S is the Ordering cost per order
H is the holding cost per unit
Substituting the values we get,
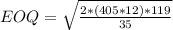
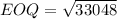
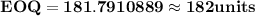
2. The annual costs of ordering, purchasing and holding the integrated chips is the sum of the cost of ordering, purchasing and holding the integrated chips.
Since the EOQ at 182 units falls in the second slab of Rich Blue Manufacturing, Bell computer can purchase chips at $325 per unit
Cost of purchasing the chips 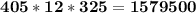
Number of orders to placed 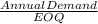
Number of orders to placed 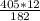
Number of orders to placed 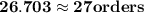
Cost of orders 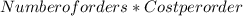
Cost of orders 
Holding Costs 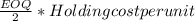
Holding Costs 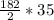
Holding Costs 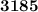
Total annual costs 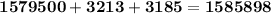
1. We need to calculate the EOQ, which holding cost at each purchase price
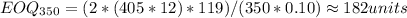
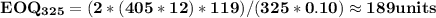
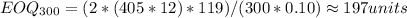
Since the EOQ lies between 100 and 199 units in all the three costs, Bell Computers can purchase the units only at $325 per unit, so its holding cost will be 10% of $325, which is $32.50 per unit.
2.2. The annual costs of ordering, purchasing and holding the integrated chips is the sum of the cost of ordering, purchasing and holding the integrated chips.
Since the EOQ at 189 units falls in the second slab of Rich Blue Manufacturing, Bell computer can purchase chips at $325 per unit
Cost of purchasing the chips 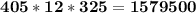
Number of orders to placed 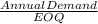
Number of orders to placed 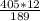
Number of orders to placed 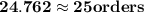
Cost of orders 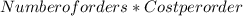
Cost of orders 
Holding Costs 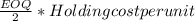
Holding Costs 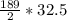
Holding Costs 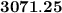
Total annual costs 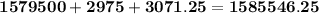

It will provide an instant answer!
