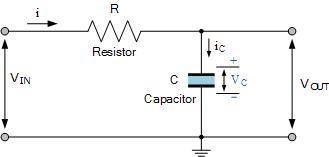
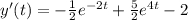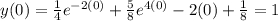Advanced Placement (AP): Solve the following differential equation with initial conditions: y =e^-2t+10e^4t ; y(0)=1, y (0)=0

Option A. Explanation: This is a second order DE, so we ll need to integrate twice, applying initial...

Solve the following differential equation with, №18011267, 06.11.2020 20:40

Biology

Conditions under which natural selection occurs in a beetle population are described in the table below: natural selection description a green and brown beetles exist in a population b brown colored beetles escape predation to live longer which factor contributes to natural selection for each condition? a. condition a and condition b represent competition. b.condition a and condition b represent inherited variation. c. condition a represents inherited variation, and condition b represents differential reproductive success. d.condition a represents

Step-by-step answer

P Answered by Specialist

5

I feel like it’s C , because brown beetles got the “good inheritance” of being brown making them less visible to the eye escaping predators

Explanation:

Biology

Conditions under which natural selection occurs in a population of iguanas are described in the table below: Natural Selection Description Condition Description A Iguanas that were good swimmers and divers had the advantage of finding food in the water over other iguanas B The larger hatchlings produced by larger female iguanas had a higher chance of survival Which factor contributes to natural selection for each condition? Condition A represents competition, and Condition B represents differential reproductive success. Condition A represents differential

Step-by-step answer

P Answered by Specialist

14

Condition A represents differential reproductive success, and Condition B represents competition.

Explanation:

I took the test 5 times

Mathematics

Imade this the highest point value, and i will give brainliest to whoever does it well and right! which of the following differential equations with initial condition yields a solution curve that exhibits modified exponential growth such that y goes to negative infinity as t goes to positive infinity? (hint: check each one by solving the differential equation quickly. remember, to solve the differential equation the quick and easy way, recall the fact that the solution to the differential equation frac{dy}{dt} = k(y-a) is y = a e^{kt} +a.

Step-by-step answer

P Answered by Specialist

The answer to this question is (d).[tex]\dfrac{dy}{dt} = 2(y-200) [/tex] with initial condition y(0) = 50======if we use the hint, we convert these all of these differential equations like so [tex]\dfrac{dy}{dt} = k(y-a) \implies y = a e^{kt} +a[/tex]so we will check each one, and then use the initial condition to solve for the constant a. we will determine if any one of the equations results in an exponential function with a behavior that is described by, "y goes to negative infinity as t goes to positive infinity" (i.e. [tex]\lim_{t \to \infty} y(t) = - \infty[/tex] ).=======checking (a) [tex]\dfrac{dy}{dt} = -2(y-200) \implies y = ae^{-2t} + 200[/tex]solving for a using initial condition y(0) = 100 (when t = 0, y = 100) [tex]\begin{aligned} 100 & = ae^{-2(0)} + 200 \\ 100 & = a + 200 \\ a & = -100 \end{aligned}[/tex]the solution to this differential equation is therefore [tex]y = -100e^{-2t} + 200[/tex]. as t approaches infinity: [tex]\begin{aligned} \displaystyle\lim_{t \to \infty} \left(-100e^{-2t} + 200\right) & = -100e^{-\infty} + 200 \\ & = 200 \end{aligned}[/tex]we used the fact that [tex]\lim_{t \to\infty} \left( e^{-2t} \right) = 0[/tex]. (e raised to a very large negative exponent approaches 0.)so this is not the answer.======checking (b) [tex]\dfrac{dy}{dt} = -3.5(y+123) \implies y = ae^{-3.5t} - 123[/tex]solving for a using initial condition y(0) = 100 (when t = 0, y = 100) [tex]\begin{aligned} 100 & = ae^{-3.5(0)} - 123 \\ 100 & = a - 123 \\ a & = 223 \end{aligned}[/tex]the solution to this differential equation is therefore [tex]y = 223e^{-3.5t} - 123[/tex]. the limit of the solution as t approaches infinity is [tex]\begin{aligned} \lim_{t\to\infty} \left( 223e^{-3.5t} - 123 \right) & = 0 - 123 \\ & = -123 \end{aligned}[/tex]this is not the answer.======checking (c) [tex]\dfrac{dy}{dt} = 3.5(y+123) \implies y = ae^{3.5t} - 123[/tex]solving for a using initial condition y(0) = 50 (when t = 0, y = 50) [tex]\begin{aligned}50 & = ae^{3.5(0)} - 123 \\ 50 & = a - 123 \\ a & = 173 \end{aligned}[/tex]therefore, the solution to this differential equation is [tex]y = 173e^{3.5t} - 123[/tex]. the limit of this solution as t approaches infinity is [tex]\begin{aligned} \lim_{t\to\infty} \left( 173e^{3.5t} - 123 \right) & = 223(\infty) - 123 \\ & = + \infty\end{aligned}[/tex]since [tex]\lim_{t \to \infty} \left(e^{3.5t }\right) = \infty[/tex]this is positive infinity. this is not the answer.======checking (d) [tex]\dfrac{dy}{dt} = 2(y-200) \implies y = ae^{2t} + 200[/tex]solving for a using initial condition y(0) = 50 (when t = 0, y = 50) [tex]\begin{aligned} 50 & = ae^{2(0)} + 200 \\ 50 & = a + 200 \\ a & = -150 \end{aligned}[/tex]therefore, the solution to this differential equation is [tex]y = -150e^{2t} + 200[/tex]. the limit of this solution as t approaches infinity is [tex]\begin{aligned} \lim_{t \to \infty} \left( -150e^{2t} + 200\right) & = -150(\infty) + 200 \\ & = -\infty \end{aligned}[/tex]the answer to this question is (d).if we did the same thing for (e), we would end up with a = 250, which wouldn't result in a +∞ limit

Mathematics

Imade this the highest point value, and i will give brainliest to whoever does it well and right! which of the following differential equations with initial condition yields a solution curve that exhibits modified exponential growth such that y goes to negative infinity as t goes to positive infinity? (hint: check each one by solving the differential equation quickly. remember, to solve the differential equation the quick and easy way, recall the fact that the solution to the differential equation frac{dy}{dt} = k(y-a) is y = a e^{kt} +a.

Step-by-step answer

P Answered by Specialist

The answer to this question is (d).[tex]\dfrac{dy}{dt} = 2(y-200) [/tex] with initial condition y(0) = 50======if we use the hint, we convert these all of these differential equations like so [tex]\dfrac{dy}{dt} = k(y-a) \implies y = a e^{kt} +a[/tex]so we will check each one, and then use the initial condition to solve for the constant a. we will determine if any one of the equations results in an exponential function with a behavior that is described by, "y goes to negative infinity as t goes to positive infinity" (i.e. [tex]\lim_{t \to \infty} y(t) = - \infty[/tex] ).=======checking (a) [tex]\dfrac{dy}{dt} = -2(y-200) \implies y = ae^{-2t} + 200[/tex]solving for a using initial condition y(0) = 100 (when t = 0, y = 100) [tex]\begin{aligned} 100 & = ae^{-2(0)} + 200 \\ 100 & = a + 200 \\ a & = -100 \end{aligned}[/tex]the solution to this differential equation is therefore [tex]y = -100e^{-2t} + 200[/tex]. as t approaches infinity: [tex]\begin{aligned} \displaystyle\lim_{t \to \infty} \left(-100e^{-2t} + 200\right) & = -100e^{-\infty} + 200 \\ & = 200 \end{aligned}[/tex]we used the fact that [tex]\lim_{t \to\infty} \left( e^{-2t} \right) = 0[/tex]. (e raised to a very large negative exponent approaches 0.)so this is not the answer.======checking (b) [tex]\dfrac{dy}{dt} = -3.5(y+123) \implies y = ae^{-3.5t} - 123[/tex]solving for a using initial condition y(0) = 100 (when t = 0, y = 100) [tex]\begin{aligned} 100 & = ae^{-3.5(0)} - 123 \\ 100 & = a - 123 \\ a & = 223 \end{aligned}[/tex]the solution to this differential equation is therefore [tex]y = 223e^{-3.5t} - 123[/tex]. the limit of the solution as t approaches infinity is [tex]\begin{aligned} \lim_{t\to\infty} \left( 223e^{-3.5t} - 123 \right) & = 0 - 123 \\ & = -123 \end{aligned}[/tex]this is not the answer.======checking (c) [tex]\dfrac{dy}{dt} = 3.5(y+123) \implies y = ae^{3.5t} - 123[/tex]solving for a using initial condition y(0) = 50 (when t = 0, y = 50) [tex]\begin{aligned}50 & = ae^{3.5(0)} - 123 \\ 50 & = a - 123 \\ a & = 173 \end{aligned}[/tex]therefore, the solution to this differential equation is [tex]y = 173e^{3.5t} - 123[/tex]. the limit of this solution as t approaches infinity is [tex]\begin{aligned} \lim_{t\to\infty} \left( 173e^{3.5t} - 123 \right) & = 223(\infty) - 123 \\ & = + \infty\end{aligned}[/tex]since [tex]\lim_{t \to \infty} \left(e^{3.5t }\right) = \infty[/tex]this is positive infinity. this is not the answer.======checking (d) [tex]\dfrac{dy}{dt} = 2(y-200) \implies y = ae^{2t} + 200[/tex]solving for a using initial condition y(0) = 50 (when t = 0, y = 50) [tex]\begin{aligned} 50 & = ae^{2(0)} + 200 \\ 50 & = a + 200 \\ a & = -150 \end{aligned}[/tex]therefore, the solution to this differential equation is [tex]y = -150e^{2t} + 200[/tex]. the limit of this solution as t approaches infinity is [tex]\begin{aligned} \lim_{t \to \infty} \left( -150e^{2t} + 200\right) & = -150(\infty) + 200 \\ & = -\infty \end{aligned}[/tex]the answer to this question is (d).if we did the same thing for (e), we would end up with a = 250, which wouldn't result in a +∞ limit

Mathematics

Consider the differential equation dy/dx = 1/3x(y-2)^2. (a) a slope field for the given differential equation is shown below. sketch the solution curve that passes through the point (0, 2), and sketch the solution curve that passes through the point (1, 0). (b) let y = f(x) be the particular solution to the given differential equation with initial condition f(1) = 0. write an equation for the line tangent to the graph of y = f(x) at x = 1. use your equation to approximate f(0.7). (c) find the particular solution y = f(x) to the given differential

Step-by-step answer

P Answered by PhD

12

A) Judging by the slope field, it would appear the solution passing through (0, 2) would just be the line y=2

. This holds up for the given ODE, since if y(x)=2

, then both sides of the ODE reduce to 0.

Since we can surmise that y=2

is an equilibrium for this ODE (that is, the derivative along this line is 0 everywhere), and the slope at (1, 0) is positive, we know that as $x\to+\infty$ , the function y(x)

will converge to 2. In other words, as

gets larger, the slope field suggests that the solution curve through (1, 0) will start to plateau and steadily approach y=2

. On the other hand, as $x\to-\infty$ , the slope field tells us that the curve would rapidly diverge off to $-\infty$ . (When you actually draw the solution, you would end up with something resembling the plot of $-e^{-x}$ .)

b) The tangent line to y=f(x)

at

, given that f(1)=0

, takes the form

$\ell(x)=f(1)+f'(1)(x-1)$
$\ell(x)=f'(1)(x-1)$

When x=1

, we have

, so

$f'(1)=\dfrac13\cdot1\cdot(0-2)^2=\dfrac43$

and so the tangent line to f(x)

at

is

$\ell(x)=\dfrac43(x-1)$

Using the tangent line as an approximation, we would find

$f(0.7)\approx\ell(0.7)=\dfrac43\left(\dfrac7{10}-1\right)=-\dfrac4{10}=-0.4$

c) The ODE is separable, so we can write

$\dfrac{\mathrm dy}{\mathrm dx}=\dfrac13x(y-2)^2\iff\dfrac{\mathrm dy}{(y-2)^2}=\dfrac x3\,\mathrm dx$

Integrating both sides gives us

$-\dfrac1{y-2}=\dfrac{x^2}6+C$

Given that y(1)=0

, we get

$-\dfrac1{0-2}=\dfrac{1^2}6+C\implies C=\dfrac13$

so the particular solution is

$-\dfrac1{y-2}=\dfrac{x^2}6+\dfrac13$

You're asked to find the solution in the form y=f(x)

, so you should solve for

. You would end up with

$y=-\dfrac6{x^2+2}+2=\dfrac{2(x^2-1)}{x^2+2}$

Mathematics

Consider the differential equation dy/dx = 1/3x(y-2)^2. (a) a slope field for the given differential equation is shown below. sketch the solution curve that passes through the point (0, 2), and sketch the solution curve that passes through the point (1, 0). (b) let y = f(x) be the particular solution to the given differential equation with initial condition f(1) = 0. write an equation for the line tangent to the graph of y = f(x) at x = 1. use your equation to approximate f(0.7). (c) find the particular solution y = f(x) to the given differential

Step-by-step answer

P Answered by PhD

12

A) Judging by the slope field, it would appear the solution passing through (0, 2) would just be the line y=2

. This holds up for the given ODE, since if y(x)=2

, then both sides of the ODE reduce to 0.

Since we can surmise that y=2

is an equilibrium for this ODE (that is, the derivative along this line is 0 everywhere), and the slope at (1, 0) is positive, we know that as $x\to+\infty$ , the function y(x)

will converge to 2. In other words, as

gets larger, the slope field suggests that the solution curve through (1, 0) will start to plateau and steadily approach y=2

. On the other hand, as $x\to-\infty$ , the slope field tells us that the curve would rapidly diverge off to $-\infty$ . (When you actually draw the solution, you would end up with something resembling the plot of $-e^{-x}$ .)

b) The tangent line to y=f(x)

at

, given that f(1)=0

, takes the form

$\ell(x)=f(1)+f'(1)(x-1)$
$\ell(x)=f'(1)(x-1)$

When x=1

, we have

, so

$f'(1)=\dfrac13\cdot1\cdot(0-2)^2=\dfrac43$

and so the tangent line to f(x)

at

is

$\ell(x)=\dfrac43(x-1)$

Using the tangent line as an approximation, we would find

$f(0.7)\approx\ell(0.7)=\dfrac43\left(\dfrac7{10}-1\right)=-\dfrac4{10}=-0.4$

c) The ODE is separable, so we can write

$\dfrac{\mathrm dy}{\mathrm dx}=\dfrac13x(y-2)^2\iff\dfrac{\mathrm dy}{(y-2)^2}=\dfrac x3\,\mathrm dx$

Integrating both sides gives us

$-\dfrac1{y-2}=\dfrac{x^2}6+C$

Given that y(1)=0

, we get

$-\dfrac1{0-2}=\dfrac{1^2}6+C\implies C=\dfrac13$

so the particular solution is

$-\dfrac1{y-2}=\dfrac{x^2}6+\dfrac13$

You're asked to find the solution in the form y=f(x)

, so you should solve for

. You would end up with

$y=-\dfrac6{x^2+2}+2=\dfrac{2(x^2-1)}{x^2+2}$

Engineering

3.3 Equation (2) for VCPP is rather difficult to prove at this time. Take it as a challenge to derive it as you learn increasingly more on the topic of differential equations. 3.4 Explain in your own words why an R-C series circuit can act approximately as an integrator as well as a differentiator and under what conditions.

Step-by-step answer

P Answered by Specialist

For an RC integrator circuit, the input signal is applied to the resistance with the output taken across the capacitor, then VOUT equals VC. As the capacitor is a frequency dependant element, the amount of charge that is established across the plates is equal to the time domain integral of the current. That is it takes a certain amount of time for the capacitor to fully charge as the capacitor can not charge instantaneously only charge exponentially.

Therefore the capacitor current can be written as:

his basic equation above of iC = C(dVc/dt) can also be expressed as the instantaneous rate of change of charge, Q with respect to time giving us the following standard equation of: iC = dQ/dt where the charge Q = C x Vc, that is capacitance times voltage.

The rate at which the capacitor charges (or discharges) is directly proportional to the amount of the resistance and capacitance giving the time constant of the circuit. Thus the time constant of a RC integrator circuit is the time interval that equals the product of R and C.

Since capacitance is equal to Q/Vc where electrical charge, Q is the flow of a current (i) over time (t), that is the product of i x t in coulombs, and from Ohms law we know that voltage (V) is equal to i x R, substituting these into the equation for the RC time constant gives:

We have seen here that the RC integrator is basically a series RC low-pass filter circuit which when a step voltage pulse is applied to its input produces an output that is proportional to the integral of its input. This produces a standard equation of: Vo = ∫Vidt where Vi is the signal fed to the integrator and Vo is the integrated output signal.

The integration of the input step function produces an output that resembles a triangular ramp function with an amplitude smaller than that of the original pulse input with the amount of attenuation being determined by the time constant. Thus the shape of the output waveform depends on the relationship between the time constant of the circuit and the frequency (period) of the input pulse.

By connecting two RC integrator circuits together in parallel has the effect of a double integration on the input pulse. The result of this double integration is that the first integrator circuit converts the step voltage pulse into a triangular waveform and the second integrator circuit converts the triangular waveform shape by rounding off the points of the triangular waveform producing a sine wave output waveform with a greatly reduced amplitude.

RC Differentiator

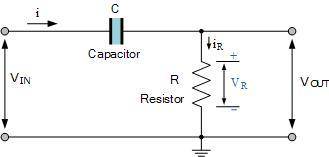
For a passive RC differentiator circuit, the input is connected to a capacitor while the output voltage is taken from across a resistance being the exact opposite to the RC Integrator Circuit.

A passive RC differentiator is nothing more than a capacitance in series with a resistance, that is a frequency dependentTherefore the capacitor current can be written as:

device which has reactance in series with a fixed resistance (the opposite to an integrator). Just like the integrator circuit, the output voltage depends on the circuits RC time constant and input frequency.

Thus at low input frequencies the reactance, XC of the capacitor is high blocking any d.c. voltage or slowly varying input signals. While at high input frequencies the capacitors reactance is low allowing rapidly varying pulses to pass directly from the input to the output.

This is because the ratio of the capacitive reactance (XC) to resistance (R) is different for different frequencies and the lower the frequency the less output. So for a given time constant, as the frequency of the input pulses increases, the output pulses more and more resemble the input pulses in shape.

We saw this effect in our tutorial about Passive High Pass Filters and if the input signal is a sine wave, an rc differentiator will simply act as a simple high pass filter (HPF) with a cut-off or corner frequency that corresponds to the RC time constant (tau, τ) of the series network.

Thus when fed with a pure sine wave an RC differentiator circuit acts as a simple passive high pass filter due to the standard capacitive reactance formula of XC = 1/(2πƒC).

But a simple RC network can also be configured to perform differentiation of the input signal. We know from previous tutorials that the current through a capacitor is a complex exponential given by: iC = C(dVc/dt). The rate at which the capacitor charges (or discharges) is directly proportional to the amount of resistance and capacitance giving the time constant of the circuit. Thus the time constant of a RC differentiator circuit is the time interval that equals the product of R and C. Consider the basic RC series circuit below.

Explanation:

3.3 Equation (2) for VCPP is rather difficult to prove at this time. Take it as a challenge to deriv