Geography : asked on jarredweatherly

12.06.2022

Which of the following types of mining is least likely to cause a loss of biodiversity

Step-by-step answer

13.12.2022, solved by verified expert

Bibin (Bibi) P B

m Master

Biology, Geography, Q&A Expert

13 338

22 231 answers

4.8 rating

Unlock the full answer

Answer:

Long wall method

Step-by-step explanation:

longwall mining Longwall mining is an underground method of excavating coal from tabular deposits, as well as soft mineral deposits such as potash. Large rectangular blocks of coal are defined during the development stage of the mine and are then extracted in a single continuous operation.

It is was helpful?

Helpful Useless

Faq

Biology

Which type of mining is likely the least harmful to the environment? a. surface mining b. placer mining c. subsurface mining d. none of the above

Step-by-step answer

P Answered by PhD

It would be placer because you are not digging up any ground..if that is not right it might be none because if you are messing with water environments you are still messing with it which could not be good

Biology

Which type of mining is likely the least harmful to the environment? a. surface mining b. placer mining c. subsurface mining d. none of the above

Step-by-step answer

P Answered by Specialist

Placer mining

Explanation:

Placer mining can be less damaging to the environment than surface mines, as the sediment is returned to the water after the minerals have been extracted.

Biology

Which type of mining is likely the least harmful to the environment? a. surface mining b. placer mining c. subsurface mining d. none of the above

Step-by-step answer

P Answered by PhD

Biology

Which type of mining is likely the least harmful to the environment? a. surface mining b. placer mining c. subsurface mining d. none of the above

Step-by-step answer

P Answered by PhD

Answer;

-Surface mining

Explanation;

-Mining involves the extraction of valuable minerals or other geological materials from the earth, commonly from an orebody, lode, vein, seam, reef or placer deposit. Despite having a large range of advantages economically, mining impacts the environment negatively because minerals are contained within the Earth. Earth must be removed in order to extract the minerals. When the minerals are close to the surface, the earth is removed, causing destruction to the shape of the land and the flora and fauna living in that area.

-Among different types of mining, surface mining is one of the method that greatly impacts the environment. It destroys all plant life in the area the mine occupies. Plants living in the area where the surface mine is to be located are removed. After the surface mine is no longer productive, plants may eventually return to the area, but typically some human efforts at reclamation are required to restore the environment to some level of productivity.

Biology

What type of mining is likely the least harmful to the environment? a.surface b.placer c.subsurface d.none of the above

Step-by-step answer

P Answered by Specialist

The Answer will be C. Subsurface.

Biology

What type of mining is likely the least harmful to the environment? a.surface b.placer c.subsurface d.none of the above

Step-by-step answer

P Answered by Master

The Answer will be C. Subsurface.

Mathematics

Blacktop Refining extracts minerals from ore mined at two different sites in Montana. Each ton of ore type 1 contains 50% copper, 10% zinc, and 15% magnesium. Each ton of ore type 2 contains 15% copper, 25% zinc, and 10% magnesium. Ore type 1 costs $90 per ton, while ore type 2 costs $120 per ton. Blacktop would like to buy enough ore to extract at least 8 tons of copper, 6 tons of zinc, and 5 tons of magnesium in the least costly manner. a. Formulate an LP model for this problem. b. Sketch the feasible region for this problem. c. Find the optimal

Step-by-step answer

P Answered by Specialist

Ore 1 = 28 tons

Ore 2 = 8 tons

Cost = $3480

Explanation:

Complete solution is provided in attached pictures. The Objective function line is dragged to the lowest edge of feasible region to obtain the optimum solution of (28,8).

That is 28 tons of Ore type-1 and 8 tons of Ore Type-2 should be ordered to incur minimum cost of $3480.

Blacktop Refining extracts minerals from ore mined at two different sites in Montana. Each ton of or

Mathematics

Blacktop Refining extracts minerals from ore mined at two different sites in Montana. Each ton of ore type 1 contains 20% copper, 20% zinc, and 15% magnesium. Each ton of ore type 2 contains 30% copper, 25% zinc, and 10% magnesium. Ore type 1 costs $90 per ton while ore type 2 costs $120 per ton. Blacktop would like to buy enough ore to extract at least 8 tons of copper, 6 tons of zinc, and 5 tons of magnesium in the least costly manner. a. Formulate an LP model for this problem. b. Sketch the feasible region for this problem. c. Find the optimal

Step-by-step answer

P Answered by Master

a) Minimize 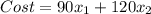Cost=90x_1+120x_2

subject to

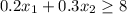
$0.2x_1+0.3x_2\geq8$

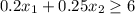
$0.2x_1+0.25x_2\geq6$

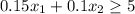
$0.15x_1+0.1x_2\geq5$

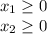
$x_1\geq0\\x_2\geq0$

b) Attached

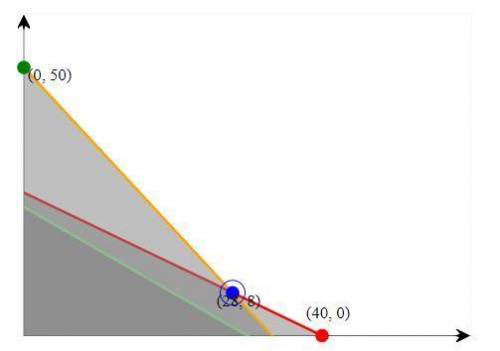
c) The optimum value that minimizes cost is x1=28 and x2=8.

Step-by-step explanation:

The objective function is the cost of extraction and needs to be minimized.

The cost of extraction is the sum of the cost of extraction of ore type 1 and the cost of extraction of ore type 2:

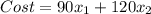
Cost=90x_1+120x_2

Being x1 the tons of ore type 1 extracted and x2 the tons of ore type 2.

The constraints are the amount of minerals that need to be in the final mix

Copper:

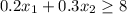
$0.2x_1+0.3x_2\geq8$

Zinc

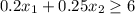
$0.2x_1+0.25x_2\geq6$

Magnesium

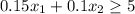
$0.15x_1+0.1x_2\geq5$

Of course, x1 and x2 has to be positive numbers.

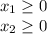
$x_1\geq0\\x_2\geq0$

The feasible region can be seen in the attached graph.

The orange line is the magnesium constraint. The red line is the copper constraint. The green line is the zinc constraint.

The optimal solution is found in one of the intersection points between two constraints that belong to the limits of the feasible region.

In this case, the cost can be calculated for the 3 points that satisfies the conditions.

The optimum value that minimizes cost is x1=28 and x2=8.

Mathematics

Step-by-step answer

P Answered by Master

Ore 1 = 28 tons

Ore 2 = 8 tons

Cost = $3480

Explanation:

Complete solution is provided in attached pictures. The Objective function line is dragged to the lowest edge of feasible region to obtain the optimum solution of (28,8).

That is 28 tons of Ore type-1 and 8 tons of Ore Type-2 should be ordered to incur minimum cost of $3480.

StudenGPT

Student Choice Task: Choose one of the following activities and post your response to the discussion board. Respond to at least one other student s response on the discussion board. Option 1: Write a 250-word response to the following questions: Do you live in the city or in the country? Do you like where you live, why or why not? Would you like to live elsewhere? Why or why not. Option 2: Create a 6-10 slide slideshow presentation sharing the following: Places you have lived or visited Interesting facts about places you have lived in or visited

Step-by-step answer

P Answered by Studen AI

Option 3: Create a 5-minute video recording yourself answering the following questions:

Question 1: What is it like where you live?

Answer: Where I live is a small town nestled in the countryside. It's a close-knit community where people know each other well. We have beautiful picturesque landscapes, with rolling hills and lush green fields. The pace of life is slower compared to cities, which gives a sense of tranquility and connection to nature. There are some cozy cafes and locally-owned shops, which adds charm to the town. Overall, it's a peaceful and serene place to reside.

Question 2: What do you wish you could change about where you live?

Answer: While I appreciate the simplicity and close community in my town, there are a few things I would like to change. Firstly, there is a limited availability of recreational activities for young people. We only have a small park and a community center that is not well-equipped. I would love to have more sports facilities or a dedicated youth center to engage the younger generation. Secondly, the public transportation system needs improvement as it is not very efficient, making it challenging to commute to nearby cities for work or leisure. Lastly, I wish there were more job opportunities locally, as many people have to commute to larger cities for employment.

Question 3: What is the most interesting place you have visited and why?

Answer: One of the most interesting places I have visited is New York City. The bustling streets, towering skyscrapers, and vibrant energy of the city captivated me. The diversity of cultures, cuisines, and attractions was truly incredible. From visiting iconic landmarks like Times Square and Central Park, to exploring museums and art galleries, there was never a dull moment. The city's fast pace and rich history made it an unforgettable experience.

Question 4: What place or event would you most like to be able to see and why?

Answer: One place I would love to visit is the Great Barrier Reef in Australia. It is the world's largest coral reef system and is renowned for its incredible biodiversity. As an avid scuba diver, I am fascinated by marine life, and being able to explore the colorful coral formations and swim alongside exotic fish would be a dream come true. The Great Barrier Reef is not only a natural wonder but also a fragile ecosystem that needs to be protected, and by visiting, I can raise awareness about its conservation.

In conclusion, while I enjoy the peacefulness and close community in my small town, there are certain aspects I wish could be improved. Exploring new places like New York City has broadened my perspective, and I aim to visit more fascinating destinations like the Great Barrier Reef in the future. Overall, embracing both the simplicity of small-town life and the exciting opportunities in larger cities can create a well-rounded and fulfilling lifestyle.

free Ask question

Today we have helped

558 students

just now

Mathematics

2x≥12
I can't figure this out

p Answered by PhD

just now

Mathematics

10-(-41)-28 what is the answer of this question

m Answered by Master

1 minute ago