The value of a car t years after it is purchased is given by the decreasing function V, where V(t) is measured in dollars. The rate of change of the car’s value in dollars per year is proportional to the car’s value. Which of the following differential equations could be used to model the value of the car, where k is a constant?

dV(t)/dt = kV(t)

Step-by-step explanation:

Since the rate of change of the car’s value in dollars per year dV(t)/dt is proportional to the car’s value V(t), ten

dV(t)/dt ∝ V(t)

dV(t)/dt = kV(t)

To get the solution to the problem we must know about differential equations.

A function that relates to one or more functions and their derivatives is known as a differential equation.

The differential equations 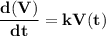used to model the value of the car, where k is a constant.

Given information:

1.)   The value of a car t years after it is purchased is given by the decreasing function V.

2.)   The rate of change of the car’s value in dollars per year is proportional to the car’s value.

3.)   k is a constant.

Solutions

1.)   The value of a car t years after it is purchased is given by the decreasing function V.

Therefore, function V for value of a car in t years is V(t).

2.)   The rate of change of the car’s value in dollars per year is proportional to the car’s value.

rate of change of the car’s value ∝ value of a car in t years

Therefore,

3.)   k is a constant.

As we know that when the proportionality symbol is removed a constant is been introduced, as it is already been given about a constant k. Therefore,

hence, the differential equations 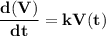can be used to model the value of the car, where k is a constant.

Learn more about differential equations: