Or
Step-by-step explanation:
For a polynomial function of lowest degree with rational real coefficients, each root has multiplicity of 1.
The polynomial has roots 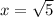 and 2 with a leading coefficient of 3.
and 2 with a leading coefficient of 3.
By the irrational root theorem of polynomials, 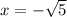 is also a root of the required polynomial.
is also a root of the required polynomial.
By the factor theorem, we can write the polynomial in factored form as:
We expand, applying difference of two squares to obtain
We expand further using the distributive property to get: