1. $33,000
2. $6077.53
3.
a) 2.72 seconds
b) 0.96 seconds
4. 189 square meters
5.
a) Average Rate of Change = 4 pounds per week, or -4
b) 160 pounds (after 5 weeks)
6.
Independent Variables = p, A, and H
Dependent Variable = T
141 beats per minute (rounded to nearest whole number)
Step-by-step explanation:
1.
The value of a tractor V(t) decreases over time, t. Its value is given by:
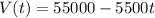
To find value of tractor after 4 years, we would need to substitute "4" into t and calculate. It is shown below:
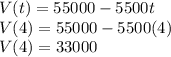
The value of the tractor after 4 years is $33,000
2.
The value of investment that is growing each year, is given by:
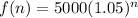
Where
5000 is the initial investment (deposit)
1.05 means a 5% growth rate per year
n is the time in years
We want the investment's value after 4 years, so n would be 4. Substituting we get our
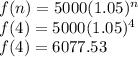
To the nearest cent, the value of the investment would be:
$6077.53
3,
The time it takes of pendulum to make one swing is given by the formula:
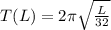
Where L is the length of the pendulum in feet
a)
If L = 6ft, the time it will take is:
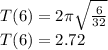
About 2.72 seconds
b)
Now, the length is 9 inches, we convert it to feet first:
9/12 = 0.75 feet
So, the time it will take:
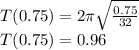
So, it will take about 0.96 seconds
4.
The area of weed after t days can be modeled by:
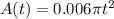
Where t is number of days
Now, we want to find area after 100 days, so let t = 100, we get:
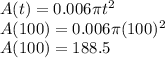
Rounded to nearest sq. m, we have the area to be:
189 square meters
5.
a)
The avg. rate of change is basically how much the program is advertising that someone can loose in a week. It says "4 pounds per week". Since decrease, we give the value of "4" and negative sign So:
Average Rate of Change = 4 pounds per week, or -4
b)
Initial weight is 180 pounds, we know 4 pounds is decreased every week when going through the program course. So, after 5 weeks,
5 * 4 = 20 pounds will be less
So, he will be:
180 - 20 = 160 pounds (after 5 weeks)
6.
The Karvonen formula is given as:
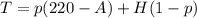
Where
T is target heart rate (in bpm)
p is the percent intensity (expressed as decimal)
A is the age (in yrs)
H is the resting heart rate (in bpm)
We need to identity the independent and dependent variables. Now, lets that a simple example:
y = 2x
Here,
x is the independent variable
y is dependent on x, so y in dependent
Similarly, if you look at the formula, you can see:
p, A, and H are all independent
T depends on them
So,
p, A, H are independent variables
T is the dependent variable
Independent Variables = p, A, and H
Dependent Variable = T
We are given
A = 35
H = 60
p = 65% = 65/100 = 0.65
Now, we want T, lets substitute and find:
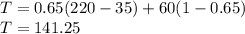
The target heart rate should be: 141 beats per minute (rounded to nearest whole number)