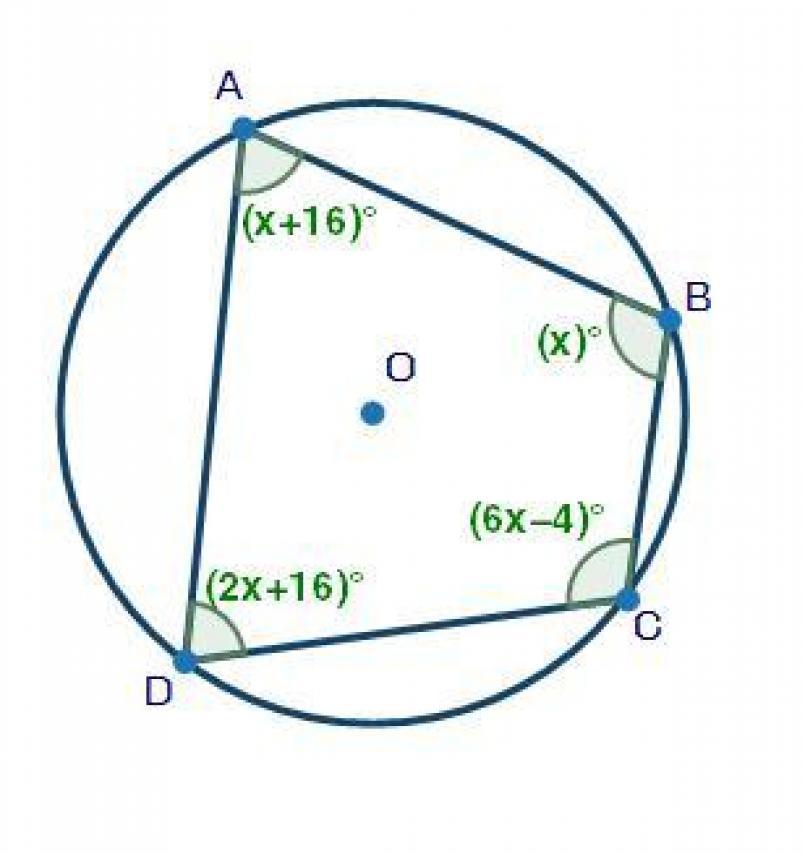
13Options:
a. (x + 16) − (6x − 4) = 180
b. (x + 16) + (x) = 90
c. (2x + 16) + (x) = 180
d. (x + 16) − (x) = 90
Answer:
c. (2x + 16) + (x) = 180
The equation that can be used to solve for angle B is (2x + 16) + (x) = 180
Explanation:
This question can be solved by using one of the circle theorems under the topic of Circle geometry.
The theorem that can be used to answer this question states thus:
" Opposite angles of a cyclic quadrilateral are supplementary"
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle.
Supplementary angles are angles that add up to 180°
To determine what equation can be used to solve for angle B,
In the given diagram, angles A and C are opposite angles of the cyclic quadrilateral and add up to 180°
Also, angles B and D are opposite angles of the cyclic quadrilateral and add up to 180°
∴ B + D = 180°
From the diagram
B = (x)° and D = (2x+16)°
∴ (x)° + (2x+16)° = 180°
Hence, the equation that can be used to solve for angle B is (2x + 16) + (x) = 180.
Other circle theorems include:
1. Angles in the same segment are equal
2. The angle at the centre is twice the angle at the circumference
3. The angle in a semicircle is a right angle etc.
21 189
rating
Get help with homework
