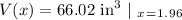
Step-by-step explanation:
Part (a)
The volume of a rectangular prism is found using the formula: V = lwh.
In order to write a formula in terms of the variable x, we need to write expressions for the length, width, and height of the rectangle.
We can say the length is the bottom of the base of the prism. To find this value, we can subtract x and x from 15 and divide this by 2, since there are two equal rectangles (base and lid).
Length:
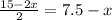
We can say the width is the side of the base of the prism. To find this value, we can subtract 2x from 10.
Width:
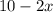
The height of the prism can be x, which is the labeled length of the rectangle next to the base and lid.
Height:

Now we are able to write a formula for volume in terms of x.
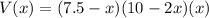
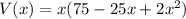
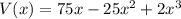
Part (b)
The domain of the volume is where x > 0, 2x < 10, and 2x < 15.
This is because our expressions for length (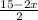 ), width (10-2x), and height (x) cannot go below 0, because you cannot have a negative value for measurement - realistically.
), width (10-2x), and height (x) cannot go below 0, because you cannot have a negative value for measurement - realistically.
Therefore, if we take into account all of these restrictions on x, the domain is where 0 < x < 5.
x cannot be > 5 since that would not satisfy 2x < 10.
The domain of V for this problem situation is D: (0, 5).
Part (c)
In order to find the maximum volume of the rectangular prism using our formula we derived, we can use the idea of optimization in calculus.
Start by taking the derivative of V(x).
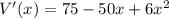
Set the derivative equal to 0. This gives us the critical point(s) in order to determine the extreme values of the function, aka where the max and min occur.
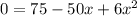
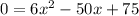
Solve for x by using the quadratic formula.
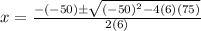
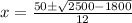
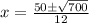
Input this into your calculator and you should get:
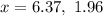
We are going to use x = 1.96 since 6.37 is NOT in the domain of V(x).
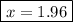
Now, since this value of x is going to give the maximum volume of this rectangular prism, or cardboard box, we can plug it back into the V(x) equation for volume to determine the maximum volume of the box.
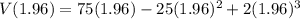
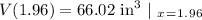
The maximum volume of the cardboard box is 66.02 in³ and the value of x that gives this is 1.96.