It is not possible for the student to receive an A grade in the class.
It is possible for the student to receive a B grade in the class.
Step-by-step explanation:
We are given that in the DBE 122 class, there are 350 possible points. These points come from 5 homework sets that are worth 10 points each and 3 exams that are worth 100 points each.
A student has received homework scores of 7, 8, 7, 5, and 8, and the first two exam scores are 81 and 80.
Firstly, we will calculate how many points have been scored by the student.
Number of possible points = 350
The points scored by the student in homework = 7 + 8 + 7 + 5 + 8 = 35 points.
The scores of the student on the two exams = 81 + 80 = 161 points
So, the total points scored by the students = 35 + 161 = 196 points.
As it is given in the question that if the grade percentage is 0.9 or higher then the student will get an A, i.e;
If the total possible points are 350 points; 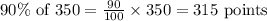
This means that the student must have to score 315 points to get an A grade.
Till the second exam, the total points scored by the students are 196 points. If the student scored full 100 marks in the third exam, then the total points scored by the student will be = 196 + 100 = 296 points.
Since 296 < 315, this means that it is not possible for the student to receive an A in the class.
Also, it is given in the question that if the grade percentage is between 0.8 and 0.9 the student will get a B, i.e, the student must obtain a minimum of 80% to get B grade.
If the total possible points are 350 points; 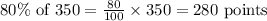
This means that the student must have to score a minimum of 280 points to get a B grade.
Till the second exam, the total points scored by the students are 196 points. If the student scored full 100 marks in the third exam, then the total points scored by the student will be = 196 + 100 = 296 points.
Since 296 > 280, this means that it is possible for the student to receive a B grade in the class.