Mathematics : asked on 6f3fe9730cc70e7740e6bdbfcf2f4f98

14.07.2020

Can you please help with numbers 19-21

0

Step-by-step answer

06.06.2023, solved by verified expert

Mathematics, English, Physics. Research Scholar at Indian Institute of Technology, Roorkee

5 423 answers

Unlock the full answer

1 students found this answer

Answer:

19) 24 units.
20) 24 cm
21) 14.7 cm

Step-by-step explanation:

19.

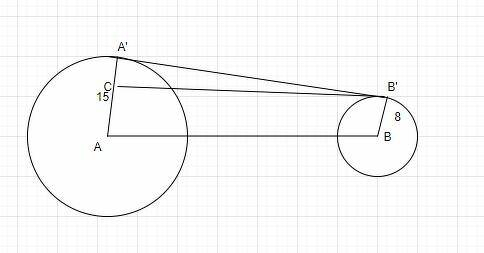
GIVEN: AA' = 15 units, BB' = 8 units and AB = 25 units.

To find: A'B'

Draw B'C = AB (ABB'C is a parallelogram)

Therefore, AC = BB' = 8 units.

CA' = 15 - 8 = 7 units.

A'CB' is a right angle traingle with B'C hypotenuse.

Using the Pythagorean theorem, we can calculate the length of the common external tangent (the side opposite to the right angle):

B'C^2 = A'B'^2 + A'C^2

25^2 = A'B'^2 + 7^2

A'B'^2 = 625 - 49 = 576

A'B' = √576 = 24 units.

Thus, the length of the common tanget = 24 units

20.

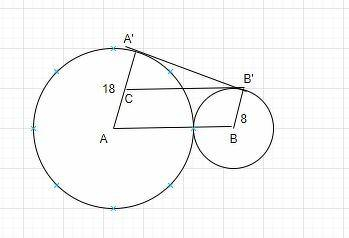
Can you please help with numbers 19-21, №16986912, 14.07.2020 19:56

GIVEN: AA' = 18 cm, BB' = 8 cm and AB = 18+8 = 26 cm.

To find: A'B'

Draw B'C = AB (ABB'C is a parallelogram)

Therefore, AC = BB' = 8 cm.

CA' = 18 - 8 = 10 cm.

A'CB' is a right angle traingle with B'C hypotenuse.

Using the Pythagorean theorem, we can calculate the length of the common external tangent (the side opposite to the right angle):

B'C^2 = A'B'^2 + A'C^2

26^2 = A'B'^2 + 10^2

A'B'^2 = 676 - 100 = 576

A'B' = √576 = 24 cm

Thus, the length of the common tanget = 24 cm

21.

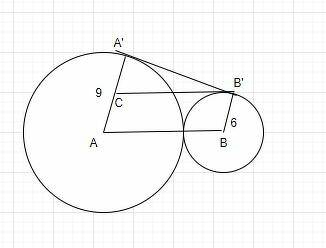
Can you please help with numbers 19-21, №16986912, 14.07.2020 19:56

GIVEN: AA' = 9 cm, BB' =6 cm and AB = 9+6 = 15 cm.

To find: A'B'

Draw B'C = AB (ABB'C is a parallelogram)

Therefore, AC = BB' = 6 cm.

CA' = 9 - 6 = 3 cm.

A'CB' is a right angle traingle with B'C hypotenuse.

Using the Pythagorean theorem, we can calculate the length of the common external tangent (the side opposite to the right angle):

B'C^2 = A'B'^2 + A'C^2

15^2 = A'B'^2 + 3^2

A'B'^2 = 225 - 9 = 216

A'B' = √216 = 14.696 cm = 14.7 cm

Thus, the length of the common tanget = 14.7 cm

It is was helpful?

Helpful Useless

Faq

Mathematics

Using the following intervals for the scores on a 30-point quiz, how many x s would fall over the interval of 19-21 on a line plot? Scores: 21, 27, 20, 29, 23, 21, 21, 27, 26, 25 Intervals: 19-21, 22-24, 25-27, and 28-30 A.1 B.4

Step-by-step answer

P Answered by Specialist

10

B. 4

Step-by-step explanation:

Interval: 19-21

Scores that are between 19 and 21 are underlined:

Scores in order: 20, 21, 21, 21, 23, 25, 26, 27, 27, 29

Mathematics

Given the following scores on a 30-point quiz, which of the following is an accurate frequency table? 21, 22, 20, 29, 25, 21, 21, 27, 26, 25 Grades 19-21 22-24 25 - 27 28-30 Frequency 4 2 2. 3 Grades 19-21 22 - 24 25 - 27 28-30 Frequency 4 1 4. 1

Step-by-step answer

P Answered by PhD

9

Table B is accurate

Step-by-step explanation:

Given

Observations: 21, 22, 20, 29, 25, 21, 21, 27, 26, 25

Required

An accurate frequency table

From both tables in the attachment; both tables use a grouped data to represent the grades.

The grouped data is as follows;

19-21

22-24

25 - 27

28-30

Breaking down these groups into bits:

19-21 :- 19, 20, 21

22-24 :- 22, 23, 24

25 - 27 :- 25, 26, 27

28-30:- 28, 29, 30

Looking up these values in the given data, we have

19-21 :- 21, 20, 21, 21

22-24 :- 22

25 - 27 :- 25, 27, 26, 25

28-30:- 29

Getting their frequencies

19-21 :- 4

22-24 :- 1

25 - 27 :- 4

28-30:- 1

Hence, the second table is accurate

Mathematics

Using the following intervals for the scores on a 30-point quiz, how many x s would fall over the interval of 19-21 on a line plot? Scores: 21, 27, 20, 29, 23, 21, 21, 27, 26, 25 Intervals: 19-21, 22-24, 25-27, and 28-30 A.1 B.4

Step-by-step answer

P Answered by Specialist

10

B. 4

Step-by-step explanation:

Interval: 19-21

Scores that are between 19 and 21 are underlined:

Scores in order: 20, 21, 21, 21, 23, 25, 26, 27, 27, 29

Mathematics

Given the following scores on a 30-point quiz, which of the following is an accurate frequency table? 21, 22, 20, 29, 25, 21, 21, 27, 26, 25 Grades 19-21 22-24 25 - 27 28-30 Frequency 4 2 2. 3 Grades 19-21 22 - 24 25 - 27 28-30 Frequency 4 1 4. 1

Step-by-step answer

P Answered by PhD

9

Table B is accurate

Step-by-step explanation:

Given

Observations: 21, 22, 20, 29, 25, 21, 21, 27, 26, 25

Required

An accurate frequency table

From both tables in the attachment; both tables use a grouped data to represent the grades.

The grouped data is as follows;

19-21

22-24

25 - 27

28-30

Breaking down these groups into bits:

19-21 :- 19, 20, 21

22-24 :- 22, 23, 24

25 - 27 :- 25, 26, 27

28-30:- 28, 29, 30

Looking up these values in the given data, we have

19-21 :- 21, 20, 21, 21

22-24 :- 22

25 - 27 :- 25, 27, 26, 25

28-30:- 29

Getting their frequencies

19-21 :- 4

22-24 :- 1

25 - 27 :- 4

28-30:- 1

Hence, the second table is accurate

Mathematics

How do you solve 19-21?

Step-by-step answer

P Answered by Specialist

Answer for question 19:

$\boxed{~x=-1 ~or~ x=-2}$

→ Step -1: Factor left side of equation:

(x+1)(x+2)=0

→ Step 2: Set factors equal to 0:

x+1=0 ~or ~x+2=0

x=-1 ~or ~x=-2

______________________________________________________

Answer for question 20:

$\boxed{~x=4 ~or ~x=-4}$

→ Step -1: Add 13 to both sides:

x^2-13+13=3+13

x^2=16

→ Step 2: Take square root:

+ $\sqrt{16}$

x=4 ~or ~x=-4

______________________________________________________

Answer for question 21:

$\boxed{~x=2 ~or~ x=-14}$

→ Step 1: Factor left side of equation:

(x-2)(x+14)=0

→ Step 2: Set factors equal to 0:

x-2=0 ~or~ x+14=0

x=2 ~or~ x=-14

Mathematics

Samantha visits her local farmers market to buy apples and oranges to make a fruit salad. she has $10.00 to spend. i need with 19-21!

Step-by-step answer

P Answered by Specialist

27

19: .26 x 38 = 9.88 so answer is 38.
20: .38 x 26 = 9.88 so answer is 26.
21: apples: .26 x 19 = 4.94 so answer is 19
oranges: .38 x 13 = 4.94 so answer is 13

Mathematics

Write the empirical relation between mean, median and mode. (1) The mean of the following distribution is 18. Find the frequency f of the class 19 - 21. Class 11-13 13-15 15-17 17-19 19-21 21-23 Frequency 3 6 9 13 f 5 23 - 25 4

Step-by-step answer

P Answered by PhD

class midpoint (m) frequency(f) fm

11-13 12 3 36

13-15 14 6 84

15-17 16 9 144

17-19 18 13 234

19-21 20 f 20f

21-23 22 5 110

23 - 25 24 4 96

∑f= 40 +f ∑fm= 704+20f

now

mean = ∑fm ÷ ∑f

18= 704 + 20f

40+f

720 + 18f= 704 + 20f

16 = 2f

f = 8

For a moderately skewed distribution it is: If a frequency distribution has a symmetrical frequency curve, the mean, median and mode are equal

Mathematics

Do 19-21 will mark brainliest

Step-by-step answer

P Answered by PhD

Question 19: x=9

Question 20: r<-6

Step-by-step explanation:

For question 19, the answer is nine because if you first add 5to both sides, it would be 18= 2r. If you divide both sides by 2, you would get 9=r.

For question 20, if you subtract 7 on each side, you would get -2r=12 if you divide -2 on each side, r would be -6.

Biology

Use this information for questions 19-21 Two mice breed. The male is heterozygous for the dominant traits of black fur and active behavior but is homozygous recessive for light eyes. The female mouse is heterozygous for dark eyes, has white fur, and displays lazy behavior. How many types of gametes does the male mouse produce?

Step-by-step answer

P Answered by PhD

The male mouse would produce four possible combinations of gametes in equal proportions which includes: BAd, Bad, bAd and bad.

Explanation:

let B- black fur, A- active behaviour and D-dark eyes

The male mouse is heterozygous for dominant traits of black fur and active behavior but is homozygous recessive for light eyes.

Thus the genotype will be: BbAadd

The female mouse is heterozygous for dark eyes, has white fur, and displays lazy behavior. thus the genotype wil be: bbaaDd

The male mouse would produce four possible combinations of gametes in equal proportions which includes: BAd, Bad, bAd and bad

Mathematics

Draw a histogram for the intervals 16-18,19-21, 22-24, and 25-27 using the following data: 26, 16, 27

Step-by-step answer

P Answered by Master

8

Answer with explanation:

Class Interval Variate Frequency

16-18 16 1

19-21 0 0

22-24 0 0

25-27 26,27 2

Draw a histogram for the intervals 16-18,19-21, 22-24, and 25-27 using the following data: 26, 16,

free Ask question

Today we have helped

444 students

just now

History

What form of
government did Lenin
convert Russia to?
Why?

p Answered by PhD

just now

Mathematics

Find the sum of each of the following series:
(a) 2 + 7 + 12 + +92

s Answered by Specialist

1 minute ago

History

How come many Americans sided with the Allied Powers even though the United States was neutral?

p Answered by PhD

1 minute ago

Mathematics

Find the degree of the monomial.
5b^7c^6

p Answered by PhD

1 minute ago

Physics

Consider a ball tossed from the ground into the air at 25 m/s. At a later time, the ball is measured to be moving downward at 11 m/s. a) Find how high the ball is off of the ground at the later time. b) Find the time interval between these two events. c) Sketch graphs of position, velocity, and acceleration versus time for the ball.

p Answered by PhD

Get help with homework

What is Studen

Studen helps you with homework in two ways:

Our base includes complete solutions from various experts

chat

Leave a question

Studen will automatically choose an expert for you.

directly

We have more than 5 000 verified experienced expert