Answers:
1) The Equation of a Line is:
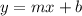 (1)
(1)
Where:
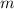 is the slope
is the slope
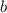 is the y-intercept
is the y-intercept
For this problem we have a given 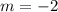 and a given
and a given 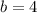
So, we only have to substitute this values in the equation (1):
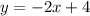
This is option B
2) Here we have to find the slope 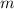 and the y-intercept
and the y-intercept 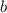 of this equation:
of this equation:
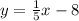
According to the explanation in the first answer related to the equation (1), the slope of this line is:
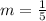
And its y-intercept is:
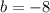
This is option C
3) We have to Equations of the Line, and we are asked if these are parallel:
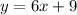 (a)
(a)
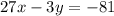 (b)
(b)
Equation (b) has to be written in the same form of (a), in the form 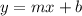 in order to be able to compare both:
in order to be able to compare both:
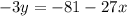
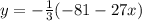
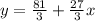
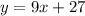 (c)
(c)
There is a rule that establishes that Two lines are parallel if they have the same slope. In this case, if we compare equations (a) and (c) we find they don’t have the same slope, then they are not parallel.
4) Here we are asked to write 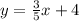 in a standard form with integers:
in a standard form with integers:
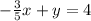
Multiply each side by 5:
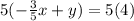
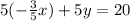
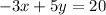
In this case none of the options apply, please check if the question was written correctly.
5) In this question we are asked to write an equation parallel to:
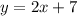 (2)
(2)
That passes through the given point (3,11). (Notice that in the Cartesian plane the points have an x-component and a y-component)
First, remember that two Equations of the line are parallel when they have the same slope. Now that this is clear, we are going to use the equation of the slope with the given point to find the parallel equation:
Equation of the slope:
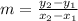 (3)
(3)
From (2) we know the slope is 2, then we only have to substitute this value and the points in (3):
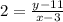
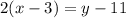
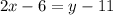
Finally:
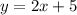
This is option B