a. 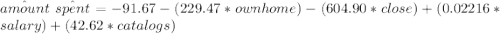
b. the expected amount spent by Amy is $1144.47
c. the expected amount that Brenda is going to spend is $1749.37
Step-by-step explanation:
(a)
From the regression output; the equation for the regression model can be written as:
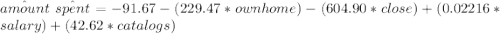
From the information given in the question;
(b)
Amy does not own a home but rent; the variables given also stated that ;
Own Home = 1 if customer owns home, 0 if renting
So for Amy ; Own Home = 0 (since it is rented)
Close = Yes(1)
Salary = $60,000
Catalogs = 12
Therefore;
the mean amount spent by Amy is by using the regression model is ;
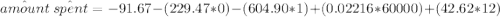
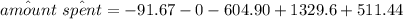
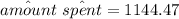
Thus; the expected amount spent by Amy is $1144.47
(c)
If Brenda has the same characteristics as Amy but does not live close to store with similar merchandise.
Then the Close for Brenda will be = No (0)
Thus; the amount spent by Brenda will be:
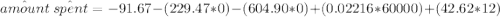
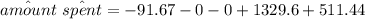
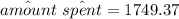
Thus, the expected amount that Brenda is going to spend is $1749.37