A polynomial is an expression of more than one term. An
expression is considered a polynomial when is has more than one term,
otherwise, it would be called a monomial. These can be combined together
through multiplication, addition and subtraction only. (Meaning no division or
fractions)
Ex.
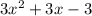
x is a variable
(There can be more than 1 variable in a term. Ex. 3xy, 4xyz, 4ab)
*A variable may be represented by letters.
2 is an exponent
3 is a constant
Those are the parts of a polynomial.
Polynomials can be categorized depending on the number of
terms and their degree.
A polynomial with two terms is called a binomial. If it has
three terms it is called a trinomial. If the expression has more than 3 terms, they
are generally called polynomials.
A polynomial can be categorized by degree as well. You can
determine the degree of a polynomial by looking at the term that has the
highest exponent.
Using the example above, you can categorize the polynomial
as a 2nd degree trinomial because 2 is the highest exponent and it
has three terms.
When you add and subtract polynomials you need to take note
of the variables. You can only subtract and add like terms, which means that
the variables and the exponents are the same.
Ex.
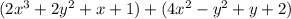
When you add these two polynomials, you can disregard the
parentheses because according to the associative property of addition, no
matter how you group the terms, the answer will be the same.
Like mentioned before you can only add and subtract like
terms. It would be easier if you just group like terms together by rearranging
the expression. Do not forget that the sign or operation comes along with them.
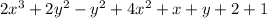
Now combine the like terms.
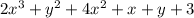
Notice that we retained the terms 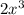 ,
, 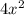 , x and y, this is because they have no similar terms.
, x and y, this is because they have no similar terms.
FOIL method is used when multiplying 2 BINOMIALS. Remember
that a binomial is an expression with 2 terms.
FOIL means:
FIRST term: first terms of each binomial.
OUTSIDE term: The two outer terms when taking the equation
as a whole.
INSIDE term: The two inner terms when taking the equation as
a whole.
LAST term: Last term of each binomial (2nd term
of each binomial)
To get the answer, you need to multiply them with their
corresponding term.
Ex. (2x+3)(x-4)
F: 2x and x (2x)(x) = 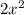
O: 2x and -4
(2x)(-4) = -8x
I: 3 and x (3)(x) = 3x
L: 3 and -4 (3)(-4) = -12
Resulting expression:
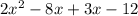 -8x and 3x are similar or like
terms, so you can combine them
-8x and 3x are similar or like
terms, so you can combine them
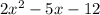
When doing multiplication with binomials, there are two
special cases you can consider doing, which follow a pattern. The first is multiplying
sum and difference.
The condition where you can apply the first special case is
the first term needs to be the same and the second term are additive inverses.
(a+b)(a-b)
The resulting expression follows this pattern 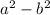
Ex. (x+3)(x-3) = 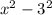 or
or 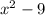
You can use FOIL to check your
F: (x)(x) = 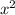
O: (x)(-3) = 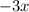
I: (3)(x) = 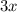
L: (3)(-3) = 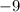
Arrange the expression:
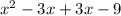 Combining -3x+3x = 0
Combining -3x+3x = 0
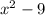
The next special case is squaring a binomial and there are two scenarios that you can consider.
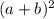 and
and 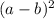
The resulting expression follows a certain pattern for each:
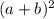 =
= 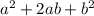
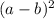 =
= 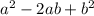
Let's use an example of each to demonstrate this and check with FOIL:
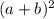
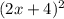
a = 2x b = +4
Let's insert that into our pattern:
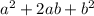
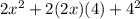
Simplify the expression:
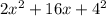
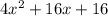
Let's check with FOIL
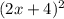 =
= 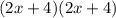
F: (2x)(2x) = 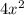
O: (2x)(4) = 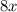
I: (4)(x) = 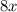
L: (4)(4) = 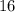
Let's arrange the terms:
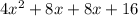
Combine the like terms
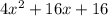
It's the same.
Now let's use the second scenario:
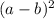

a = 2x b = -4
Let's insert that into our pattern:
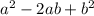
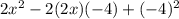
Simplify the expression:
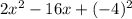
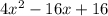
Let's check with FOIL
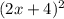 =
= 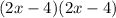
F: (2x)(2x) = 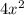
O: (2x)(-4) = 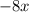
I: (-4)(x) = 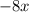
L: (-4)(-4) = 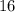
Let's arrange the terms:
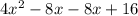
Combine the like terms
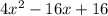
It's the same.