The age at which small breed dogs are fully housebroken follows a Normal distribution with mean ms = 6 months and standard deviation ss = 2.5 months. The age at which large breed dogs are fully housebroken follows a Normal distribution with mean mL = 4 months and standard deviation sL = 1.5 months. Let xS – xL represent the sampling distribution. Be sure show all work and conditions. Let the sample size for both sets be 25 dogs. Should we be surprised if the sample mean housebroken age for the small breed dogs is at least 2.5 months more than the sample mean housebroken age for the large breed dogs? Explain your answer.

This measure is just 0.17 standard deviations from the mean, so we should not be surprised.

Step-by-step explanation:

Normal probability distribution

When the distribution is normal, we use the z-score formula.

In a set with mean 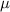and standard deviation 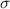, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

If the z-score is lower than -2, or higher than 2.5, the score of X is considered unusual.

Subtraction of normal variables:

When we subtract normal variables, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of the variances.

Let xS – xL represent the sampling distribution.

Mean s 6, means L 4. So

Standard deviation s is 2.5, for L is 1.5. So

Should we be surprised if the sample mean housebroken age for the small breed dogs is at least 2.5 months more than the sample mean housebroken age for the large breed dogs? Explain your answer.

We have to find the z-score for X = 2.5. So

This measure is just 0.17 standard deviations from the mean, so we should not be surprised.

The answer is in the image 

y=2x+15

where y=Value of coin

x=Age in years

Value of coin after 19 years=2*19+15

=$53

Therefore, Value after 19 years=$53

F=ma

where F=force

m=mass

a=acceleration

Here,

F=4300

a=3.3m/s2

m=F/a

    =4300/3.3

    =1303.03kg

F=ma

where F=force

m=mass

a=acceleration

Here,

F=4300

a=3.3m/s2

m=F/a

    =4300/3.3

    =1303.03kg

Approximately it is aqual to 1300kg

The answer is in the image 

Here,

tip=18%of $32

tip=(18/100)*32

=0.18*32

=$5.76

Total payment=32+5.76=$37.76

The answer is in the image 

The answer is in the image 

Area of rectangle= L*b

here,

L=12.4 cm

b= 8.8 cm

A= L*b

= 12.4 * 8.8 = 109.12 cm^2