The correct answers are:
(1) Option (a) 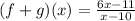
(2) Option (b) 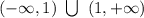
(3) Option (d) 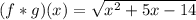
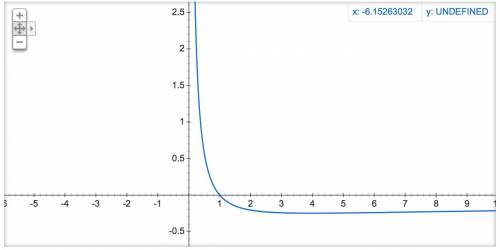
(4) Graph is attached with the answer along with the explanation (below)!
(5) Option (b) 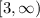
Explanations:
(1) Given Data:
f(x) = 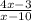
g(x) = 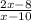
Required = (f+g)(x) = ?
The expression (f+g)(x) is nothing but the addition of f(x) and g(x). Therefore, in order to find (f+g)(x), we need to add both the given functions as follows:
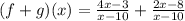
Now we need to simplify the above equation as follows:
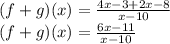
Hence the correct answer is 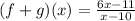 Option (a)
Option (a)
(2) Given Data:
f(x) = 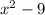
g(x) = 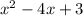
Before finding the domain of the expression 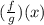 , we need to first evalute that expression as follows:
, we need to first evalute that expression as follows:
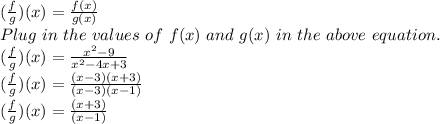
Now we need to put the denominator equal to zero in order to know what values of x should not be in the domain of this function:
x-1 = 0
x = 1
It means that the domain of 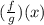 is all real numbers EXCEPT x = 1. The (closed) parentheses " ) " or "(" means that the number is not included in the domain. Therefore, we can write that the domain of
is all real numbers EXCEPT x = 1. The (closed) parentheses " ) " or "(" means that the number is not included in the domain. Therefore, we can write that the domain of 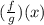 is
is 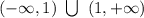 (Option b)
(Option b)
(3) Given Data:
f(x) = 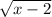
g(x) = 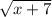
Required = (f*g)(x) = ?
The expression (f*g)(x) is nothing but the multiplication of f(x) and g(x). Therefore, in order to find (f*g)(x), we need to multiply both the given functions as follows:
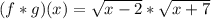
Now we need to simplify the above equation as follows:
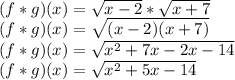 (Option d)
(Option d)
(4) Given Data:
f(x) = 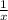
g(x) = 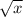
Required = The graph of (f-g)(x) = ?
Before plotting the graph let us evalute it first. (f-g)(x) is the subtraction of g(x) from f(x). Mathematically, we can write it as:
(f-g)(x) = 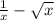
Now simplify:
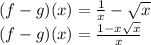
Look at the graph attached with this answer. As you can see, at x=0, the graph shoots up! As at x=0, the value of function approaches to infinity.
(5) Given Data:
f(x) = 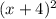
g(x) = 3
Required = Range of (f+g)(x) = ?
Before finding the range of (f+g)(x), we first need to write the function:
(f+g)(x) = 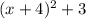
Now that we have written the function, the next step is to find the inverse of this function in order to obtain the range.To find the inverse, swap x with y, and y with x and put (f+g)(x) = y as follows:
(f+g)(x) = y = 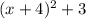
Now swap:
x = 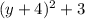
Now solve for y:
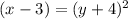
Take square-root on both sides:
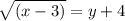
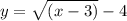
As you know that the square root of negative numbers are the complex numbers, and in range, we do not include the complex numbers. Therefore, the values of x should be greater or equal to 3 to have the square-roots to be the real numbers. Therefore,
Range of (f+g)(x) = 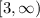 (Option b)
(Option b)
Note: "[" or "]" bracket is used to INCLUDE the value. It means that 3 is included in the range.