1.a. 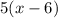
2.d=
3.c.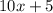
4.c.The quotient of some number and six.
5.a.The quotient of three times some number and five
6.b.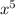
Step-by-step explanation:
1.We are given that verbal expression ''five times the difference of a number and six''
We have to find its algebraic expression
Let x be the number
Difference of x and 6=x-6
We are multiplying difference of x and 6 by 5
Then we get
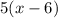
Option a is true
2.Verbal expression ''nine less than some number ''
Let k be the some number
Nine less than some number k
=
Option d is true.
3.Five more than the product of ten and some number .
Let x be the some number
Product of 10 and some number x
Then we get 10 x
Now, 5 more than the product of 10 and x
Then, we get an algebraic expression
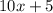
Hence, option c is true.
4.Given algebraic expression
Fraction with variable x in numerator and 6 in the denominator .
We have to find its verbal expression
The quotient of some number and six.
Hence, option c is true.
5.We are given that an algebraic expression
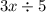
We have to find its verbal expression
The quotient of three times some number and five
Where x is some number in algebraic expression.
Hence, option a is true.
6.We are given that verbal expression
''Some number to the power of 5''
We have to find the algebraic expression
Let x be the some number
Then , the algebraic expression
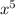
Hence, option b is true.