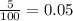Clarkson University surveyed alumni to learn more about what they think of Clarkson. One part of the survey asked respondents to indicate whether their overall experience at Clarkson fell short of expectations, met expectations, or surpassed expectations. The results showed that 5% of the respondents did not provide a response, 26% said that their experience fell short of expectations, and 65% of the respondents said that their experience met expectations. (a) If we chose an alumnus at random, what is the probability that the alumnus would say their experience surpassed expectations

(a) The probability that a randomly selected alumnus would say their experience surpassed expectations is 0.05.

(b) The probability that a randomly selected alumnus would say their experience met or surpassed expectations is 0.67.

Step-by-step explanation:

Let's denote the events as follows:

A = Fell short of expectations

B = Met expectations

C = Surpassed expectations

N = no response

Given:

P (N) = 0.04

P (A) = 0.26

P (B) = 0.65

(a)

Compute the probability that a randomly selected alumnus would say their experience surpassed expectations as follows:

Thus, the probability that a randomly selected alumnus would say their experience surpassed expectations is 0.05.

(b)

The response of all individuals are independent.

Compute the probability that a randomly selected alumnus would say their experience met or surpassed expectations as follows:

Thus, the probability that a randomly selected alumnus would say their experience met or surpassed expectations is 0.67.

0.04

Step-by-step explanation:

We are given that

The probability  that the alumnus did not provide response=5%

The probability  that the alumnus did not provide response=

The probability that the alumnus would say their experience  fell short of expectations=26%=0.26

The probability that the alumnus would say their experience met expectations=65%=0.65

We have to find the  probability that the alumnus would say their experience surpassed expectations.

We know that

Sum of all probabilities =1

Using the property

The  probability that the alumnus would say their experience surpassed expectations=1-(0.05+0.26+0.65)

The  probability that the alumnus would say their experience surpassed expectation=0.04

Step-by-step explanation:

The question is incomplete. The complete question is:

Clarkson University surveyed alumni to learn more about what they think of Clarkson. One part of the survey asked respondents to indicate whether their overall experience at Clarkson fell short of expectations, met expectations, or surpassed expectations. The results showed that 4% of respondents did not provide a response, 26% said that their experience fell short of expectations, 65% of the respondents said that their experience met expectations (Clarkson Magazine, Summer, 2001). If we chose an alumnus at random, what is the probability that the alumnus would say their experience surpassed expectations? If we chose an alumnus at random, what is the probability that the alumnus would say their experience met or surpassed expectations?

Solution:

Probability = number of favorable outcomes/number of total outcomes

From the information given,

The probability that respondents did not provide a response, P(A) is 4/100 = 0.04

The probability that a respondent said that their experience fell short of expectations, P(B) is 26/100 = 0.26

The probability that a respondent said that their experience met expectations, P(C) is 65/100 = 0.65

A) Adding all the probabilities, it becomes 0.04 + 0.26 + 0.65 = 0.95

Therefore, the probability,P(D) that a respondent said that their experience surpassed expectations is 1 - 0.95 = 0.05

B) The event of a randomly chosen respondent saying that their experience met expectations and that their experience surpassed expectations are mutually exclusive because they cannot occur together. It means that P(C) × P(D) = 0

Therefore, the probability of P(C) or P(D) is 0.65 + 0.05 = 0.7

SI=(P*R*T)/100

P=2000

R=1.5

T=6

SI=(2000*1.5*6)/100

=(2000*9)/100

=180

Neil will earn interest of 180

The answer is in the image 

The answer is in the image 

Salesperson will make 6% of 1800

=(6/100)*1800

=108

Salesperson will make $108 in $1800 sales

The solution is given in the image below

Speed=Distance/time

Here,

distance=15m

time=1sec

speed=15/1=15m/sec

Distance=Speed*time

time=15min=15*60sec=900sec

Distance travelled in 15 min=15*900=13,500m

=13500/1000 km=13.5Km