What is Irrational Root Theorem? Explain and, №17887556, 12.03.2020 03:20

Mathematics

Dennis, Emily, and Fernando want to find the zeros of the polynomial p(x)=x3+6x2+9x. Each student worked independently and presented his or her results to the group. Dennis used the Rational Root Theorem to identify all zeros of p(x). According to this theorem he stated that the zeros of p(x) are ±1, ±3, and ±9. Emily used the greatest common factor and perfect-square trinomial methods to factor p(x) as p(x)=x(x+3)2. She applied the definition of zeros and found that the zeros of p(x) are 0 and −3. Fernando used the greatest common factor and perfect-square

Step-by-step answer

P Answered by PhD

1

Fernando’s response is incorrect because he inappropriately applied the Rational Root Theorem. Dennis’ response is incorrect. According to the Fundamental Theorem of Algebra, the polynomial p(x) cannot have six roots, or zeros, because it is only of degree 3. Emily’s response is correct because she correctly factored the polynomial, and correctly used the definition of zeros to reach her answer.

Step-by-step explanation:

The Rational Root Theorem offers a list of possible rational roots. Each needs to be tested to see if it is an actual rational root. Fernando and Dennis made inappropriate assumptions about what the Rational Root Theorem allowed them to conclude.

Mathematics

Dennis, Emily, and Fernando want to find the zeros of the polynomial p(x)=x3+6x2+9x. Each student worked independently and presented his or her results to the group. Dennis used the Rational Root Theorem to identify all zeros of p(x). According to this theorem he stated that the zeros of p(x) are ±1, ±3, and ±9. Emily used the greatest common factor and perfect-square trinomial methods to factor p(x) as p(x)=x(x+3)2. She applied the definition of zeros and found that the zeros of p(x) are 0 and −3. Fernando used the greatest common factor and perfect-square

Step-by-step answer

P Answered by PhD

1

Fernando’s response is incorrect because he inappropriately applied the Rational Root Theorem. Dennis’ response is incorrect. According to the Fundamental Theorem of Algebra, the polynomial p(x) cannot have six roots, or zeros, because it is only of degree 3. Emily’s response is correct because she correctly factored the polynomial, and correctly used the definition of zeros to reach her answer.

Step-by-step explanation:

The Rational Root Theorem offers a list of possible rational roots. Each needs to be tested to see if it is an actual rational root. Fernando and Dennis made inappropriate assumptions about what the Rational Root Theorem allowed them to conclude.

Mathematics

What is Irrational Root Theorem? Explain and give examples.

Step-by-step answer

P Answered by PhD

if the irrational sum of a plus the square root of b is the root of a polynomial with rational coefficients, then a minus the square root of b, which is also an irrational number, is also a root of that polynomial.

Step-by-step explanation: Look it up

Mathematics

gary, Heather, and Irene want to find the zeros of the polynomial P(x). They evaluate the polynomial for different values and find: P(−1)=0 P(0)=1 P(2+3–√)=0 Each student interprets this information separately and presents his or her conclusions to the group. Gary concludes that since P(−1) and P(2+3–√) equal 0, 2 zeros of P(x) are −1 and 2+3–√. By the Irrational Root Theorem, 2−3–√ is also a zero of P(x). Heather concludes that since P(0)=1, 1 zero of P(x) is 1. There isn t enough information to determine any other zeros of P(x). Irene concludes

Step-by-step answer

P Answered by PhD

The answer is given below

Step-by-step explanation:

A number is said to be a zero of a polynomial if when the number is substituted into the function the result is zero. That is if a is a zero of polynomial f(x), therefore f(a) = 0.

Since P(−1)=0 P(0)=1 P(2+√3)=0, therefore -1 and 2+√3 are zeros of the polynomial.

Gary is right because there are 2 known zeros of P(x) which are −1 and 2+√3. Also 2 - √3 is also a root. From irrational root theorem, irrational roots are in conjugate pairs i.e. if a+√b is a root, a-√b is also a root.

Heather is not correct because if P(0) = 1, it means that 0 is not a root. It does not mean that 1 is a zero of P(x)

Irene is correct. since P(−1) and P(2+3–√) equal 0, 2 zeros of P(x) are −1 and 2+√3. They may be other zeros of P(x), but there isn't enough information to determine any other zeros of P(x)

Mathematics

Step-by-step answer

P Answered by Master

335

1)
f(x) = 4x^2 − 25
f(x) = 4x^2 − 25 =0 implies 4x²=25, and x²=25/4, so the possible roots are
x=sqrt(25/4= 5/2 or x= -sqrt(25/4)= -5/2
so the answer is D.Yes.

2)
g(x) = 4x^2 + 25=0 implies 4x²= -25 and since i²= -1 (complex number)
we can write 4x²= -25= 25i² so the possible root is x= sqrt(25i²/4)=5i/2 or x= -sqrt(25i²/4)=-5i/2
the answer is A. No, this polynomial has complex roots
3)
h(x) = 3x^2 − 25=0 implies 3x²=25, x²=25/3 so the possible roots are x= -sqrt(25/3)= -5/sqrt3 or x=sqrt(25/3)=5/sqrt3
the answer is B. No, this polynomial has irrational roots

Mathematics

Step-by-step answer

P Answered by Specialist

335

1)
f(x) = 4x^2 − 25
f(x) = 4x^2 − 25 =0 implies 4x²=25, and x²=25/4, so the possible roots are
x=sqrt(25/4= 5/2 or x= -sqrt(25/4)= -5/2
so the answer is D.Yes.

2)
g(x) = 4x^2 + 25=0 implies 4x²= -25 and since i²= -1 (complex number)
we can write 4x²= -25= 25i² so the possible root is x= sqrt(25i²/4)=5i/2 or x= -sqrt(25i²/4)=-5i/2
the answer is A. No, this polynomial has complex roots
3)
h(x) = 3x^2 − 25=0 implies 3x²=25, x²=25/3 so the possible roots are x= -sqrt(25/3)= -5/sqrt3 or x=sqrt(25/3)=5/sqrt3
the answer is B. No, this polynomial has irrational roots

Mathematics

Apolynomial function, f(x), with rational coefficients has roots of –2 and square root of 3. the irrational conjugates theorem states that which of the following must also be a root of the function?

Step-by-step answer

P Answered by PhD

26

if 2 + √3 is an irrational root to a polynomial, then its irrational conjugate 2- √3 is also.

Step-by-step explanation:

Given : A polynomial function, f(x), with rational coefficients has roots of –2 and square root of 3.

To find : which of the following must also be a root of the function?

Solution : We have root of f(x) = 2 +√3.

By the irrational conjugates theorem : it state that states that if a + √b is an irrational root to a polynomial, then its irrational conjugate a - √b is also

root.

Therefore, if 2 + √3 is an irrational root to a polynomial, then its irrational conjugate 2- √3 is also.

Mathematics

Apolynomial function, f(x), with rational coefficients has roots of –2 and square root of 3. the irrational conjugates theorem states that which of the following must also be a root of the function?

Step-by-step answer

P Answered by PhD

26

if 2 + √3 is an irrational root to a polynomial, then its irrational conjugate 2- √3 is also.

Step-by-step explanation:

Given : A polynomial function, f(x), with rational coefficients has roots of –2 and square root of 3.

To find : which of the following must also be a root of the function?

Solution : We have root of f(x) = 2 +√3.

By the irrational conjugates theorem : it state that states that if a + √b is an irrational root to a polynomial, then its irrational conjugate a - √b is also

root.

Therefore, if 2 + √3 is an irrational root to a polynomial, then its irrational conjugate 2- √3 is also.

Mathematics

Brainliest asap & 44 points 1.which of the following number are rational? choose any that apply a.-4 b. 3/10 c. 4. d. e. none - all numbers listed are irrational. 2. is 81 a perfect square? why/why not? * - give me an short answer. 3. determine the length from the wall to the base of the ladder. * the triangle picture is for this one a. 5 b.11 c. 18 d. 25 4. estimate the value of √52. explain how you use perfect squares to come up with your answer. no explanation will not receive credit! * - short answer 5. every rational number is a square

Step-by-step answer

P Answered by PhD

4

ANSWER TO QUESTION 1

A rational number is any number that can be written in the form,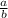 $\frac{a}{b}$ , where and 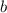are integers and $b\ne 0$ .

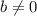We can rewrite 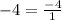$-4=\frac{-4}{1}$ .

Therefore option A is a rational number.

Option B is obviously a rational number because it is already in the form 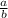$\frac{a}{b}$ .

Option C cannot be written in the form 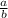$\frac{a}{b}$ because the decimal place does not repeat or recur and it does not terminate also.

Therefore 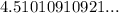4.51010910921... is not a rational number.

As for option D, the decimal places recurs or repeats and it does not terminate. We can rewrite in the form,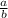 $\frac{a}{b}$ .

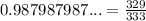$0.987987987...=\frac{329}{333}$ hence it is a rational number.

ANSWER TO QUESTION 2

Yes 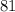is a perfect square.

All numbers whose square roots are perfect squares are rational numbers.

If we raise 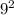$9^{2}$ we get .

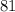In order words if we take the square root of 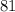we get a rational number.

That is 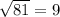$\sqrt{81} =9$

ANSWER TO QUESTION 3

Let the length from the wall to the base of the ladder be m.

The from Pythagoras Theorem,

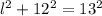
l^2+12^2=13^2

This implies that,

l^2+144=169

We add the additive inverse of 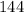144 to both sides to obtain,

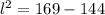
l^2=169-144

l^2=25

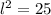
We take the positive square root of both sides to obtain,

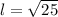
$l=\sqrt{25}$

l=5 .

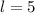The correct answer is A.

ANSWER TO QUESTION 4

We wan to estimate 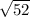$\sqrt{52}$ .

The highest perfect square that can be found in 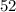is .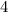

We rewrite to obtain,

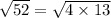$\sqrt{52} =\sqrt{4\times 13}$ .

We now split the square root sign to obtain,

$\sqrt{52} =\sqrt{4}\times \sqrt{13}$ .

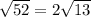$\sqrt{52} =2\sqrt{13}$ .

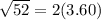$\sqrt{52} =2(3.60)$ .

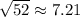$\sqrt{52} \approx 7.21$ .

ANSWER TO QUESTION 5.

The statement, every rational number is q square root is false.

We only need at least a counterexample to show that, the above statement is false.

Let be any real number.

Then 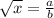$\sqrt{x} =\frac{a}{b}$ , where and 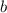are integers.

This implies that 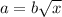$a=b\sqrt{x}$

Base on this final equation, can only be an integer if is a perfect number. Hence not every rational number is a square root because some numbers aren't perfect squares.

The correct answer is C

ANSWER TO QUESTION 6.

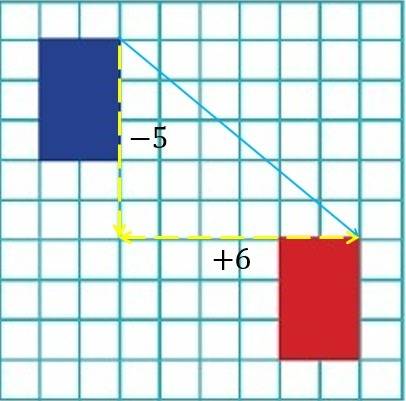
To find the translation vector that maps the blue rectangle on the red rectangle, we draw a vector connecting any two corresponding points as shown in the diagram.

The vector has horizontal component of 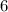and a vertical component of .

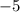Therefore the mapping is 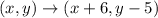$(x,y)\rightarrow(x+6,y-5)$ . The correct answer is D.

ANSWER TO QUESTION 7

Figure A accurately represents the Pythagorean Theorem because

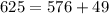
625=576+49

This implies that

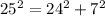
25^2=24^2+7^2

We can see that the hypotenuse square is equal to the sum of the squares of the lengths of the two shorter legs.

Recall that, 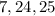7,24,25 are Pythagorean triples.

Brainliest asap & 44 points 1.which of the following number are rational? choose any that appl

Mathematics

You can buy jars of the same jam in 2 sizes large jar:440g for £1.54 small jar:340g for £1.26 By considering the price per gram, work out which jar is the best value for money. Working must be shown

Step-by-step answer

P Answered by PhD

Answer: 440 grams for 1.54 is the better value
Explanation:
Take the price and divide by the number of grams
1.54 / 440 =0.0035 per gram
1.26 / 340 =0.003705882 per gram
0.0035 per gram < 0.003705882 per gram

What is Irrational Root Theorem? Explain and give examples.

Step-by-step answer

Faq

Try asking the Studen AI a question.