The answers are as follows:
TrueFalseFalseFalseFalse
Step-by-step explanation:
Let us look at the statements one by one
1. The additive inverse of 10 is -10.
The additive inverse of a number is the opposite of a number with respect to sign.
The sum of a number and its additive inverse is zero.
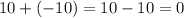
This statement is true.
2. Zero is a positive number.
Zero is neither a positive number nor a negative number. It is only used as reference to decide whether a number is positive or negative.
This statement is false.
3. To divide two unlike signs, the quotient is always positive.
When two unlike signs are divided, the answer will be negative as division involves multiplication, and multiplication of two numbers with unlike signs will always be negative.
This statement is false.
4. Commutative Property states that:
a + (b + c ) = (a + b ) + c
Commutative property deals with two numbers or variables only. The property with three numbers or varibales is associative property. Hence,
This statement is false.
5. One is the identity element of for addition.
Additive identity is a number that when added to a number x, the result will always be x. Zero is additive identity.
Hence,
This statement is false.
The answers are as follows:
TrueFalseFalseFalseFalse