Step-by-step explanation:
Hello!
1)
The variable of interest is
X: level of toxin ergovaline on the grass after being treated with Moose saliva.
>The parameter of interest is the population mean of the level of ergovaline on grass after being treated with Moose saliva: μ
The best point estimate for the population mean is the sample mean:
>X[bar]=0.183 Sample average level of ergovaline on the grass after being treated with Moose saliva.
Assuming that the sample comes from a normal population.
>There is no information about the sample size takes to study the effects of the Moose saliva in the grass. Let's say that they worked with a sample of n=20
Using the Student-t you can calculate the CI as:
X[bar] ±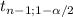 
* 
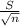
Where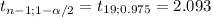 
0.183 ± 2.093 * (0.016/√20)
[0.175;0.190]
Using a 95% confidence level you'd expect that the interval [0.175;0.190] will contain the true average of ergovaline level of grass after being treated with Moose saliva.
2)
The information of a study that shows how much does the consumption of canned soup increase urinary BPA concentration is:
Consumption of canned soup for over 5 days increases the urinary BPA more than 1000%
75 individuals consumed soup for five days (either canned or fresh)
The study reports that a 95% confidence interval for the difference in means (canned minus fresh) is 19.6 to 25.5 μg/L.
>This experiment is a randomized comparative experiment.
Out of the 75 participants, some randomly eat canned soup and some randomly eaten fresh soup conforming to two separate and independent groups that were later compared.
>The parameter of interest is the difference between the population mean of urinary BPA concentration of people who ate canned soup for more than 5 days and the population mean of urinary BPA concentration of people that ate fresh soup for more than 5 days.
>Using a 95% confidence level you'd expect that the interval 19.6 to 25.5 μg/L would contain the value of the difference between the population mean of urinary BPA concentration of people who ate canned soup for more than 5 days and the population mean of urinary BPA concentration of people that ate fresh soup for more than 5 days.
> If the sample had been larger, then you'd expect a narrower CI, the relationship between the amplitude of the CI and sample size is indirect. Meaning that the larger the sample, the more accurate the estimation per CI is.
3)
> The parameter of interest is Average Long-Term Weight Gain Overeating for just four weeks can increase fat mass and weight over two years later of people with an average age of 26 years old.
> The only way of finding the true value of the parameter is if you were to use the information of the whole population of interest, this is making all swedes with an average age of 26 increase calorie intake by 70% (mostly by eating fast food) and limit their daily activity to a maximum of 5000 steps per day and then measure their weight gain over two years. since this es virtually impossible to do, due to expenses and size of the population, is that the estimation with a small but representative sample is conducted.
>
n= 18
X[bar]= 6.8 lbs
S= 1.2
X[bar] ± 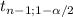* (S/√n)
6.8 ± 2.101 * (1.2/√18)
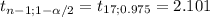
[6.206;7.394]
With a 95% confidence level, you'd expect that the interval [6.206;7.394] will contain the true value of the Average Long-Term Weight Gain Overeating for just four weeks can increase fat mass and weight over two years later of people with an average age of 26 years old.
>
The margin of error of the interval is
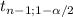* (S/√n)= 2.101 * (1.2/√18)= 0.59
With a 95% it is expected that the true value of the Average Long-Term Weight Gain Overeating for just four weeks can increase fat mass and weight over two years later of people with an average age of 26 years old. will be 0.59lbs away from the sample mean.
I hope it helps
0
helpful
rating
Get help with homework
