Evaluate the equation. f + 14 2/7= 23, №17887920, 30.08.2022 19:46

Mathematics

Evaluate the equation. f + 14 2/7= 23 A. f=8 B. f= 8 5/7 C. f=9 D. f=9 5/7

Step-by-step answer

P Answered by PhD

C

Step-by-step explanation:

f+98/7=23

f=161/7-98/7=63/7=9

C

Mathematics

Evaluate the equation. f + 14 2/7= 23

Step-by-step answer

P Answered by PhD

Third item in the list

Step-by-step explanation:

Third function: f(x) = x + 9. If we substitute 14 for x, we get f(14) = 14 + 9 = 23.

Step-by-step explanation:

Mathematics

The director of training for an equipment manufacturing company is interested in determining whether different training methods have an affect on the productivity of assembly line employees. She randomly assigns 42 newly hired employees into two groups of 21. The first group receives an on-line training program and the second receives a team based training program. At the end of the training, the employees are evaluated on the time (in seconds) that it takes to assemble a part. The results follow. A hypothesis test is made to see if there is a

Step-by-step answer

P Answered by Specialist

The null hypothesis is that there is no difference between the mean time it takes an online trained employee or a team-based trained employee to assemble the given part

Step-by-step explanation:

The information the director of the equipment manufacturing company is interested in determining is weather the productivity of assembly line employees is affected by the method used in their training

The total number newly hired employees in the sample = 42

The number of newly hired employees that receive training online = 21

The number of newly hired employees that receive training in a team = 21

The given data of the result of the time it takes an employee to assemble a part is presented as follows;

On-Line 19.4, 16.7, 20.7, 19.3, 21.8, 16.8, 14.1, 17.7, 16.1, 19.8, 16.8, 19.3, 14.7, 16.0, 16.5, 17.7, 16.2, 17.4, 16.4, 16.8, 18.5

Team; 22.4, 13.8, 18.7, 18.0, 19.3, 20.8, 15.6, 17.1, 18.0, 28.2, 21.7, 20.8, 30.7, 24.7, 23.7, 17.4, 23.2, 20.1, 12.3, 15.2, 16.0

The mean time for the of the on-line trained employee, 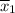$\overline x_1$ = 17.55714

The standard deviation of the time for the of the on-line trained employee, s₁ = 1.93328

The mean time for the of the team based trained employee, 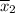$\overline x_2$ = 19.89048

The standard deviation of the time for the of the team based trained employee, s₂ = 4.5667

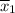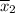
The null hypothesis, H₀: $\overline x_1$ = $\overline x_2$

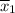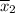
The alternative hypothesis, Hₐ: $\overline x_1$ ≠ $\overline x_2$

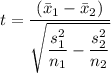
$t=\dfrac{(\bar{x}_{1}-\bar{x}_{2})}{\sqrt{\dfrac{s_{1}^{2} }{n_{1}}-\dfrac{s _{2}^{2}}{n_{2}}}}$

Therefore, we have;

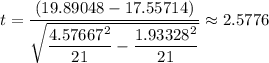
$t=\dfrac{(19.89048 - 17.55714)}{\sqrt{\dfrac{4.57667^{2}}{21} - \dfrac{1.93328^{2} }{21}}} \approx 2.5776$

The degrees of freedom, df = n₁ - 1 = 21 - 1 = 20

At 95% confidence level, we have α = 1 - 0.95 = 0.05, and t = 2.086

Therefore, given that the test statistic is larger than the critical 't' value, we reject the null hypothesis. There is sufficient statistical evidence to show that there is a difference between the mean time of assembly value for the on-line trained and team-based employee

Mathematics

Need asap which of the following expressions is equivalent to (-)? 3 · -7 -7 · 3 (-7)3 3-7 according to the order of operations, which of the following operations should be completed first in the following expression? 2(5 - 3)^2 + 6^2 multiply (5 - 3) by 2 square (5 - 3) simplify (5 - 3) add (5 - 3) to 6^2 select all that apply. which expressions are equal to five to the third power ? 5^3 3 · 3 · 3 · 3 · 3 5 · 5 · 5 125 15 243 3^5 the expression -8 · -8 · -8 · -8 can be expressed as -8^4 (-8)^4 -(8^4) what is the value of -6^2? -36 36 -12 12 find

Step-by-step answer

P Answered by Master

27

1) (-7)3

2) PEMDAS; simplify (5-3)

3) 5^3, 5x5x5 and 125

4) -8^4

5) 36

6) 7

7) -100

8) 30

There ya go! Pretty sure they're all right!