What is the domain and range?
f(x) = 2x^3 – 2

hope this answer helps

Can u mark this as brainliest

1.

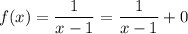
x-1 = 0  for  x = 1

so:

Vertical asymptote: x = 1

Domain:  Dom f = R\{1}  {or: Dom f = (-∞, 1)∪(1, ∞)}

Horizontal asymptote:  y = 0

Range:    Ran f=R\{0}  {or: Ran f = (-∞, 0)∪(0, ∞)}

2.

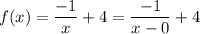
x-0 = 0  for  x = 0

so:

Vertical asymptote: x = 0

Domain:  Dom f = R\{0}  {or: Dom f = (-∞, 0)∪(0, ∞)}

Horizontal asymptote:  y = 4

Range:    Ran f=R\{4}  {or: Ran f = (-∞, 4)∪(4, ∞)}

3.

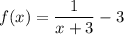
x+3 = 0  for  x = -3

so:

Vertical asymptote: x = -3

Domain:  Dom f = R\{-3}  {or: Dom f = (-∞, -3)∪(-3, ∞)}

Horizontal asymptote:  y = -3

Range:    Ran f=R\{-3}  {or: Ran f = (-∞, -3)∪(-3, ∞)}

4.

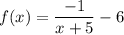
x+5 = 0  for  x = -5

so:

Vertical asymptote: x = -5

Domain:  Dom f = R\{-5}  {or: Dom f = (-∞, -5)∪(-5, ∞)}

Horizontal asymptote:  y = -6

Range:    Ran f=R\{-6}  {or: Ran f = (-∞, -6)∪(-6, ∞)}

4.

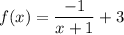
x+1 = 0  for  x = -1

so:

Vertical asymptote: x = -1

Domain:  Dom f = R\{-1}  {or: Dom f = (-∞, -1)∪(-1, ∞)}

Horizontal asymptote:  y = -6

Range:    Ran f=R\{3}  {or: Ran f = (-∞, 3)∪(3, ∞)}

5.

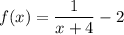
x+4 = 0  for  x = -4

so:

Vertical asymptote: x = -4

Domain:  Dom f = R\{-4}  {or: Dom f = (-∞, -4)∪(-4, ∞)}

Horizontal asymptote:  y = -2

Range:    Ran f=R\{-2}  {or: Ran f = (-∞, -2)∪(-2, ∞)}

There don't seem to be any limits/asymptotes to the function.

The graph would look something similar to this:

Tell us the value of the variable to solve

The graph is attached btw

9514 1404 393

  see attached

Step-by-step explanation:

For values of x less than zero, the graph of the function is a graph of the line

  y = -x

Because the function is defined by this expression at x=0, there will be a solid dot at the end of the line there, at (0, 0).

__

For values of x greater than 0, the graph of the function is a graph of the line

  y = -x -2

This line has the same -1 slope as before, but has a y-intercept of -2. The function is not actually defined as (0, -2), so there is an open circle at the end of the line there.

Tell us the value of the variable to solve

The graph is attached btw

see attached for a graph

domain and range: all real numbers

The function is written in slope-intercept form, showing that it has a slope of -3 and a y-intercept of +7. The y-intercept (0, 7) is a point on the line, as is a point 1 unit to the right and down 3 units, (1, 4).

The graph will be the line through these two points.

_____

As with any odd-degree polynomial function, both domain and range are all real numbers: (-∞, ∞).

Domain={R} Range={R}

Step-by-step explanation:

The function is a lineal function and every lineal function´s domain and rage is the set real numbers.

In order to sketch the function you only need to know 2 points od the function and unite them with a straight line. You can know them replacing x for a number and calculating f(x). I did it for x=0 and x=3

Now you have defining 2 point

P1=(0,3)

P2=(3,4)

I added an image of the function sketched

Graph of the following function is attached with the answer.

Domain : ( - ∞ , + ∞ )

Range : ( 3 , + ∞ )

Step-by-step explanation:

Domain of any quadratic equation is from negative infinity to positive infinity under no restrictions.

So, Domain : ( - ∞ , + ∞ )

The Range of any function can be calculated easily if there is just one term with variable. The method to find Range by that method is explained with the example as follows:

Therefore the Range of is [ 3 , + ∞ )

(NOTE : [a,b] means all the numbers between 'a' and 'b' including 'a' and 'b'.

(a,b) means all the numbers between 'a' and 'b' excluding 'a' and 'b'.

(a,b] means all the numbers between 'a' and 'b' including only 'b' not 'a'.

[a,b) means all the numbers between 'a' and 'b' including only 'a' not 'b'.

{a,b} means only 'a' and 'b'.

{a,b] or (a,b} doesn't mean anything. )

(a) Graph : In attachment

(b) Domain: (-∞,∞)

(c) Range: (-∞,∞)

Step-by-step explanation:

Given:

It is a linear function.

For sketch:

Put x=3 into f(x) to get y

f(3) = 2 - 3 = -1

Point (3,-1)

Put x=-3 into f(x) to get y

f(3) = -2 - 3 = -5

Point (-3,-5)

Plot the points on graph and join the points. Please find the attachment.

For domain:

It is input value of x where function is well defined.

Domain: All real number

For range:

It is output value of y.

Range: All real number.