The perimeter of an equilateral triangle is 60 m.the area is

173.21m^2

Step-by-step explanation:

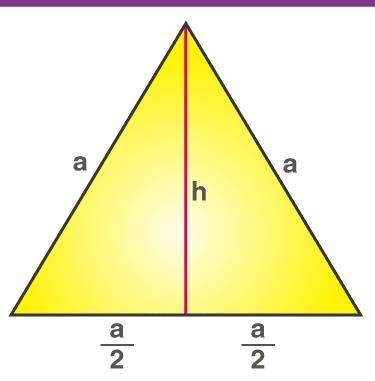
So lets figure out how to find the formula for the area of a equilateral triangle.

We can immediatly notice that a equilaterial triangle is really just two right triangles merged together at their heights.

This means that the total area of the equilaterial triangle is equivelent to finding the area of 2 right triangles. this would make the formula:

This is a fairly simple formula, and works out nicely since our normal right triangle formula for area of   must be multiplied by 2 since there are two right triangles.

The problem is, how we will actually find h, the height.

Each side length of a equilateral triangle equals 1/3 of the perimeter, meaning that each side length is 20.

W, the width of each right triangle is 1/2 of the side length of the equilateral triangle, meaning that the width equals 10.

We also know that the hypotenuse of the triangle is equal to the side length of the equilateral triangle, which means that the hypotenuse equals 20.

We can use this to figure out our unknown height, which we can then use to find our area.

We can figure out this height using teh pythagreon theorm, since

, which we can rewrite to get:

Now we can plug in our hypotenuse and width to solve:

=

=

=

Height = 17.321

Now we can solve for the area using the formula from above,

=

So our area equals 173.21!

Hope this helps! :3

The area of the triangle is 173 squared meters.

Step-by-step explanation:

An equilateral triangle has all sides equal to each other.

Finding the length of each side of the triangle.

Like I said before, in an equilateral triangle all the sides are equal. The perimeter of a triangle is every side added together. Since each side is equal, you will divide 60 (the perimeter) by 3 (the number of sides).

Each side is equal to 20 meters.

Finding the area of the triangle

To find the area of a triangle you need the formula:

A is the area, b is the base, and h is the height.

b = 20

h = 17.3

Multiply what is in the parenthesis first

Multiply 346 by 1

Divide 346 by 2

The area of the triangle is 173 squared meters.

Step-by-step explanation:

An equilateral triangle has all sides equal to each other.

Finding the length of each side of the triangle.

Like I said before, in an equilateral triangle all the sides are equal. The perimeter of a triangle is every side added together. Since each side is equal, you will divide 60 (the perimeter) by 3 (the number of sides).

Each side is equal to 20 meters.

Finding the area of the triangle

To find the area of a triangle you need the formula:

A is the area, b is the base, and h is the height.

b = 20

h = 17.3

Multiply what is in the parenthesis first

Multiply 346 by 1

Divide 346 by 2

see below

Step-by-step explanation:

if its perimeter is 60 each side is 60/3 = 20.

Its height will be 10√3 so area is 20 * 10√3 / 2 = 100√3

see below

Step-by-step explanation:

if its perimeter is 60 each side is 60/3 = 20.

Its height will be 10√3 so area is 20 * 10√3 / 2 = 100√3

The answer is in the image