Write the equation of a line that is parallel, №18010161, 06.01.2020 17:43

Mathematics

Write the equation of a line that is parallel to the given line. 1. y =- 4x

Step-by-step answer

P Answered by Master

Step-by-step explanation:

A line that is parallel will have the same slope as the reference line. The slope-intercept form of a straight line equation is:

y = mx + b,

where m is the slope and y is the y-intercept (the value of y when x=0),

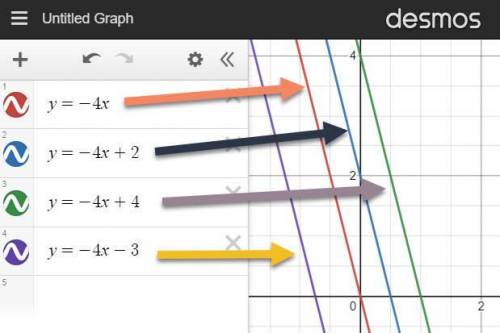
The line y = -4x has a slope of -4 and a y-intercept of 0 (it crosses the y axis when x = 0).

That means any line with the form y = -4x + b will be parallel, since the slopes are both -4.

All that is needed is to choose a value for b, the y-intercept, to be different than 0. Pick any number - all resulting lines will be parallel. I'll chose b = 2.

y = -4x + 2 is parallel to y = -4x

See attached image for these two lines, plus two more I added with different values of b.

Write the equation of a line that is parallel to the given line.
1. y =- 4x

Mathematics

Write the equation of the line passing through the given point that is parallel to the given line 1. y=2/3x - 2, (-3,4) 2.y=-2x +7y =14 (-7,-3)

Step-by-step answer

P Answered by Master

1

Answer for question #1: y= $\frac{2x}{3}$ + 6

Step-by-step explanation:

1. Find the equation of the line parallel to the line y=2x/3−2 passing through the point (−3,4).

The equation of the line in the slope-intercept form is y=2x/3−2.

The slope of the parallel line is the same: m=23.

So, the equation of the parallel line is y=2x/3+a.

To find a, we use the fact that the line should pass through the given point: 4=(23)⋅(−3)+a.

Thus, a=6.

Therefore, the equation of the line is y=2x/3+6.

y=2x/3+6.

Mathematics

Iwill give brainliest to fastest i know i already posted this but ! 17. write y = -2/3x + 2 in standard form using integers. a. -2x - 3y = 6 b. 2x + 3y = 6 c. 2x - 3y = 2 d. 2x + 3y = 2 18. write an equation for the line that is parallel to the given line and passes through the given point. y = 3x + 7; (2, 10) a. y = 3x + 11 b. y = 3x + 4 c. y = -3x + 4 d. y = (-1/3)x + 4 19. tell whether the lines for each pair of equations are parallel, perpendicular, or neither. the two equations are y = -2x + 4 and -5x + 10y = 5. a. parallel b. perpendicular

Step-by-step answer

P Answered by PhD

13

17. y = -2/3x + 2
2/3x + y = 2
2x + 3y = 6 <==

18. y = 3x + 7slope is 3. A parallel line will have the same slope.

y = mx + b
slope(m) = 3
(2,10)...x = 2 and y = 10
now sub and find b, the y int
10 = 3(2) + b
10 = 6 + b
10 - 6 = b
4 = b
so ur equation is : y = 3x + 4 <===

19. - 5x + 10y = 5
10y = 5x + 5
y = 1/2x + 1/2...slope is 1/2

y = -2x + 4slope is -2

1/2 and -2 are negative reciprocals of each otherso ur lines are perpendicular

20. y = -1/4x + 8slope is -1/4

-2x + 8y = 4
8y = 2x + 4
y = 1/4x + 1/2...slope here is 1/4

different slope and different y intercepts ...neither parallel or perpendicular

21. slope in the equation is 8/3. A perpendicular line will have a slope of -3/8.

y - y1 = m(x - x1)
slope(m) = -3/8
(-2,3)...x1 = -2 and y1 = 3
now we sub
y - 3 = -3/8(x - (-2) =
y - 3 = -3/8(x + 2) <==

Mathematics

12. the table shows the height of a plant as it grows. which equation in point-slope form gives the plant s height at any time (1 point) time (months) | plant height (cm) 2 | 16 4 | 32 6 | 48 8 | 64 (a). y - 16 = 8(x - 2) (b). y - 16 = 8x - 2 (c). y + 16 = 8(x + 2) (d). the relationship is nonlinear 14. write y = (-5/8)x + 3 in standard form using integers (1 point) (a). 5x + 8y = -24 (b). 5x + 8y = 24 (c). 5x - 8y = 24 (d). -5x + 8y = 24 15. write an equation for the line that is parallel to the given line and passes through the given point (1

Step-by-step answer

P Answered by Specialist

Ques 12)

Time (months) | Plant Height (cm)

2 | 16

4 | 32

6 | 48

8 | 64

Now, we see that the line will pass through (2,16) and (4,32)

Now, the equation of line passing through (a,b) and (c,d) is given by:

$y-b=\dfrac{d-b}{c-a}\times (x-a)$

Here (a,b)=(2,16) and (c,d)=(4,32)

Hence, the equation of line is:

$y-16=\dfrac{32-16}{4-2}\times (x-2)\\\\y-16=\dfrac{16}{2}\times (x-2)\\\\y-16=8\times (x-2)$

The relationship is clearly linear since we can relate them as:

y=8x

Hence, option: A is correct:

(A). y - 16 = 8(x - 2)

Ques 14)

y = (-5/8)x + 3

In standard form it is:

$y=\dfrac{-5}{8}x+3\\\\\\y=\dfrac{-5x+8\times 3}{8}\\\\8y=-5x+24\\\\5x+8y=24$

Hence, option: B is correct.

Ques 15)

y = 3x + 7; (2, 10)

As the line is parallel hence the slope must be same. (i.e. slope of the line y=mx+c is m.

So, here slope=3)

Now,

The line also passes through (2,10).

Hence, the equation is:

y=3x+4

( since, when x=2

y=3×2+4=6+4=10)

Ques 16)

y = -2x + 4 -------------(1)

-5x + 10y = 5-------------(2)

On solving second equation we have:

$-5x+10y=5\\\\10y=5x+5\\\\y=\dfrac{1}{2}x+\dfrac{1}{2}$

slope of first line (m)= -2

slope of second line (m')= 1/2

As m.m'=-1

Hence, the lines are perpendicular.

Ques 17)

y = -1/4x + 10 ---------(1)

-2x + 8y = 6-------(2)

On converting equation (2) we have:

$-2x+8y=6\\\\8y=2x+6\\\\y=\dfrac{2}{8}x+\dfrac{6}{8}\\\\y=\dfrac{1}{4}x+\dfrac{3}{4}$

As slope of first line is(m): -1/4

and that of second line is(m'): 1/4

Now,

mm'=-1

then the lines are perpendicular.

and if m=m' then lines are parallel.

Hence, here the answer is neither.

Ques 18)

y - 4 = 5/2 (x + 3); (-7, 8)

slope of this line is: 5/2

As the line is perpendicular hence it's slope will be: -2/5

Also it passes through (-7,8) hence, the equation is:

(C). y - 8 = -2/5 (x + 7)

Mathematics

Iwill give brainliest to fastest i know i already posted this but ! 17. write y = -2/3x + 2 in standard form using integers. a. -2x - 3y = 6 b. 2x + 3y = 6 c. 2x - 3y = 2 d. 2x + 3y = 2 18. write an equation for the line that is parallel to the given line and passes through the given point. y = 3x + 7; (2, 10) a. y = 3x + 11 b. y = 3x + 4 c. y = -3x + 4 d. y = (-1/3)x + 4 19. tell whether the lines for each pair of equations are parallel, perpendicular, or neither. the two equations are y = -2x + 4 and -5x + 10y = 5. a. parallel b. perpendicular

Step-by-step answer

P Answered by PhD

13

17. y = -2/3x + 2
2/3x + y = 2
2x + 3y = 6 <==

18. y = 3x + 7slope is 3. A parallel line will have the same slope.

y = mx + b
slope(m) = 3
(2,10)...x = 2 and y = 10
now sub and find b, the y int
10 = 3(2) + b
10 = 6 + b
10 - 6 = b
4 = b
so ur equation is : y = 3x + 4 <===

19. - 5x + 10y = 5
10y = 5x + 5
y = 1/2x + 1/2...slope is 1/2

y = -2x + 4slope is -2

1/2 and -2 are negative reciprocals of each otherso ur lines are perpendicular

20. y = -1/4x + 8slope is -1/4

-2x + 8y = 4
8y = 2x + 4
y = 1/4x + 1/2...slope here is 1/4

different slope and different y intercepts ...neither parallel or perpendicular

21. slope in the equation is 8/3. A perpendicular line will have a slope of -3/8.

y - y1 = m(x - x1)
slope(m) = -3/8
(-2,3)...x1 = -2 and y1 = 3
now we sub
y - 3 = -3/8(x - (-2) =
y - 3 = -3/8(x + 2) <==

Mathematics

12. the table shows the height of a plant as it grows. which equation in point-slope form gives the plant s height at any time (1 point) time (months) | plant height (cm) 2 | 16 4 | 32 6 | 48 8 | 64 (a). y - 16 = 8(x - 2) (b). y - 16 = 8x - 2 (c). y + 16 = 8(x + 2) (d). the relationship is nonlinear 14. write y = (-5/8)x + 3 in standard form using integers (1 point) (a). 5x + 8y = -24 (b). 5x + 8y = 24 (c). 5x - 8y = 24 (d). -5x + 8y = 24 15. write an equation for the line that is parallel to the given line and passes through the given point (1

Step-by-step answer

P Answered by Specialist

Ques 12)

Time (months) | Plant Height (cm)

2 | 16

4 | 32

6 | 48

8 | 64

Now, we see that the line will pass through (2,16) and (4,32)

Now, the equation of line passing through (a,b) and (c,d) is given by:

$y-b=\dfrac{d-b}{c-a}\times (x-a)$

Here (a,b)=(2,16) and (c,d)=(4,32)

Hence, the equation of line is:

$y-16=\dfrac{32-16}{4-2}\times (x-2)\\\\y-16=\dfrac{16}{2}\times (x-2)\\\\y-16=8\times (x-2)$

The relationship is clearly linear since we can relate them as:

y=8x

Hence, option: A is correct:

(A). y - 16 = 8(x - 2)

Ques 14)

y = (-5/8)x + 3

In standard form it is:

$y=\dfrac{-5}{8}x+3\\\\\\y=\dfrac{-5x+8\times 3}{8}\\\\8y=-5x+24\\\\5x+8y=24$

Hence, option: B is correct.

Ques 15)

y = 3x + 7; (2, 10)

As the line is parallel hence the slope must be same. (i.e. slope of the line y=mx+c is m.

So, here slope=3)

Now,

The line also passes through (2,10).

Hence, the equation is:

y=3x+4

( since, when x=2

y=3×2+4=6+4=10)

Ques 16)

y = -2x + 4 -------------(1)

-5x + 10y = 5-------------(2)

On solving second equation we have:

$-5x+10y=5\\\\10y=5x+5\\\\y=\dfrac{1}{2}x+\dfrac{1}{2}$

slope of first line (m)= -2

slope of second line (m')= 1/2

As m.m'=-1

Hence, the lines are perpendicular.

Ques 17)

y = -1/4x + 10 ---------(1)

-2x + 8y = 6-------(2)

On converting equation (2) we have:

$-2x+8y=6\\\\8y=2x+6\\\\y=\dfrac{2}{8}x+\dfrac{6}{8}\\\\y=\dfrac{1}{4}x+\dfrac{3}{4}$

As slope of first line is(m): -1/4

and that of second line is(m'): 1/4

Now,

mm'=-1

then the lines are perpendicular.

and if m=m' then lines are parallel.

Hence, here the answer is neither.

Ques 18)

y - 4 = 5/2 (x + 3); (-7, 8)

slope of this line is: 5/2

As the line is perpendicular hence it's slope will be: -2/5

Also it passes through (-7,8) hence, the equation is:

(C). y - 8 = -2/5 (x + 7)

Mathematics

Write an equation for the line that is parallel to the given line and passes through the given point y = 5x + 10; (2, 14) a) y = 1/5x + 4 b) y = -1/5x - 4 c) y = 5x - 68 d) y = 5x + 4

Step-by-step answer

P Answered by PhD

2

D

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

y = 5x + 10 is in this form with slope m = 5

• Parallel lines have equal slopes, hence

y = 5x + c ← is the partial equation

to find c substitute (2, 14) into the partial equation

14 = 10 + c ⇒ c = 14 - 10 = 4

y = 5x + 4 ← equation of parallel line → D

Mathematics

Write an equation for the line that is parallel to the given line and passes through the given point y=5x+10; (2,14) y = 1/5x+4 y = 5x+4 y = -1/5x - 4 y=5x-68

Step-by-step answer

P Answered by Specialist

10

Y = 5x+4. The slope is the same, 5, making them parallel, and when you plug in 2 for x you get 14

Mathematics

Write an equation parallel to the given line. write an equation perpendicular to the given line. 22. y= - 5x 23. y= 1/3x -1 24. 2x - 4y = 3

Step-by-step answer

P Answered by PhD

Please, post just one question at a time. I am arbitrarily focusing on #24 this time thru.
2x-3
2x - 4y = 3 can easily be solved for y: 2x-3=4y, or y =
4

The slope of this line is m = 2/4, or m = 1/2.

We need the equation of a new line parallel to this one. Use the slope-intercept form of the equation of a straight line: y = mx + b.

Let m = 1/2 and arbitrarily choose y-intercept b = 0. Then we have

y = (1/2)x + 0, or y = (1/2)x.

Want the equation of a line perpendicular to 2x - 4y = 3?

We already know that the slope of this given line is 1/2. The slope of a line perpendicular to this given line is the neg. reciprocal of 1/2, or m = -2.

Again, use the slope-intercept formula y = mx + b:

y = -2x + 0 (my choice of b = 0 is arbitrary; could have chosen some other value for b)

Mathematics

Write an equation for the line that is parallel to the given line and passes through the given point. given line: y= 2x + 4 given point: (3, 8) a.) y = 2x + 2 b.) y = 2x + 6 c.) y = -2x + 6 d.) y = - 1/2x + 2

Step-by-step answer

P Answered by PhD

Parallel lines have the same slope.

If y = 2x + 4, then parallel line has equal y = 2x + b.

The line passes throught the point (3, 8). Put the coordinates of the point to the equation of a line:

8 = 2(3) + b

8 = 6 + b subtract 6 from both sides

2 = b

A) y = 2x + 2