1) a. CI = 0.426 < p < 0.574
2) c. CI = 2.74% < p < 6.524%
3) a. CI = 20 < μ < 22
4) c. CI = 81.11 < μ < 85.09
5) b. CI = 76.21 < μ < 89.79
6) d. $453.59 < μ < $874.69
7) d. CI = $559 < σ < $1953.3
8) c. CI = $3.96 < σ < $6.72
9) c. 6.22 ft < σ < 12.59 ft
10) d. 0.19 oz < σ < 0.72 oz
Step-by-step explanation:
The Confidence Interval, CI are given as follows
For the population proportion
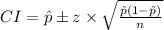
1) 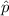 = 55/110 = 0.5
= 55/110 = 0.5
z at 88% = ±1.56
a. CI = 0.426 < p < 0.574
2) 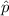 = 31/669 = 0.5
= 31/669 = 0.5
z at 98% = ±2.326
c. CI = 2.74% < p < 6.524%
3) Here we have unknown population standard deviation, so we find the t interval
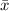 = 21
= 21
n = 130
s = 3.0
Confidence level = 98%
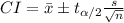
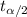 = ±2.356
= ±2.356
CI = 20.380 < μ < 21.62
Rounding up gives;
a. CI = 20 < μ < 22
4) Similarly here we have;
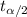 = ±1.699 and
= ±1.699 and
c. CI = 81.11 < μ < 85.09
5) Here
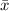 = 83
= 83
s = 13.5
n = 30
Confidence level = 99%
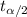 = ±2.76 and
= ±2.76 and
b. CI = 76.21 < μ < 89.79
6) In the question, we have
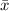 = $664.14
= $664.14
s = $297.29
n = 14
Confidence level = 98%
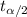 = ±2.65 and
= ±2.65 and
CI = $453.56 < μ < $874.72
d. $453.59 < μ < $874.69
7) The confidence interval for a population standard deviation is given by the following relation;
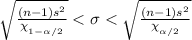
Here
n = 9
x = $3959
s = $886
Therefore we have
d. CI = $559 < σ < $1953.3
8) Here we have;
n = 41
x = $108
s = $5
Therefore;
c. CI = $3.96 < σ < $6.72
9) Here we have;
n = 29
x = 65 ft
s = 8.5 ft
Therefore we have
CI = 6.3 ft < σ < 12.73 ft
c. 6.22 ft < σ < 12.59 ft
10) Here we have
n = 8
s = 0.301188123
d. 0.19 oz < σ < 0.72 oz.