A composite function is the combination of multiple functions.
The correct answers are:
Find the composite of the functions.
The inverse of f(x) = 3x is
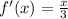
.All answers are trueThe inverse of
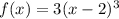
is:
![f^{-1}(x) =2 + \sqrt[3]{\frac x3}](/tpl/images/0024/3730/50983.png)
The inverse of
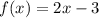
is
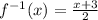
1. Test for inverse function
To test if two functions are inverse of one another, we simply find their composites.
Assume the functions are g(x) and h(x).
We simply test for 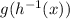 and
and 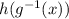
If they are equal, then both functions are inverse functions
2. Inverse of f(x) = 3x
Rewrite as:
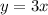
Swap y and x
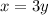
Make y the subject
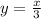
Hence, the inverse function is: 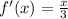
3. True statements
A function has unique ordered pairs; so, it will pass the vertical line test.
Because it has unique ordered pairs, the inverse function will pass the vertical line tests, and the horizontal line tests.
Hence;
(b) All answers are correct
4. Inverse of 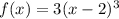
Rewrite as:
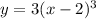
Swap x and y
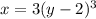
Solve for y: Divide both sides by 3
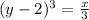
Take cube roots of both sides
![y -2 = \sqrt[3]{\frac x3}](/tpl/images/0024/3730/ce5ae.png)
Add 2 to both sides
![y =2 + \sqrt[3]{\frac x3}](/tpl/images/0024/3730/e04e4.png)
Hence, the inverse function is: ![f^{-1}(x) =2 + \sqrt[3]{\frac x3}](/tpl/images/0024/3730/50983.png)
5. The inverse of 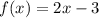
Rewrite as:
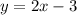
Swap x and y
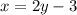
Solve for y: Add 3 to both sides
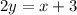
Divide both sides by 2
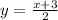
Hence, the inverse function is: 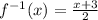
Read more about inverse functions at:
link