ANSWER TO QUESTION 1
The given function is 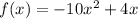 . We want to find the derivative of this function at
. We want to find the derivative of this function at 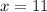 .
.
The derivative of this function is given by,
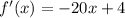
We now have to substitute 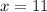 in to
in to 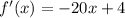 to obtain,
to obtain,
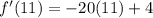
This implies that,
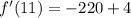
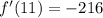
Ans: A
ANSWER TO Q2.
The given limit is 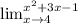 .
.
The function whose limit we are finding is a polynomial function. Since polynomial function are continuous everywhere, the limiting value is always equal to the functional value.
Thus, 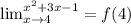
This implies that,
Thus, 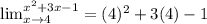 .
.
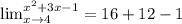
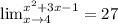
Ans: A.
ANSWER TO Q3
The given function is 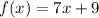 .
.
We want to find the derivative of this function at 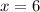 .
.
We must first of all differentiate this function to obtain,
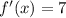
We can see that the derived function is constant, therefore value of  will still give us
will still give us 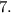
This implies that,
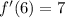
Ans: A
ANSWER TO Q4.
See attachment
ANSWER TO Q5.
The given function is 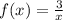 .
.
To find the derivative of this function at,
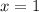 , we must first differentiate this function.
, we must first differentiate this function.
But let us rewrite the rational function as a power function so that it will be easier to differentiate using the power rule of differentiation.
That is,
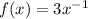 .
.
We differentiate now to obtain,
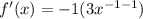
This implies that,
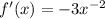
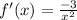
At 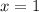
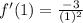
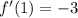
Ans: A
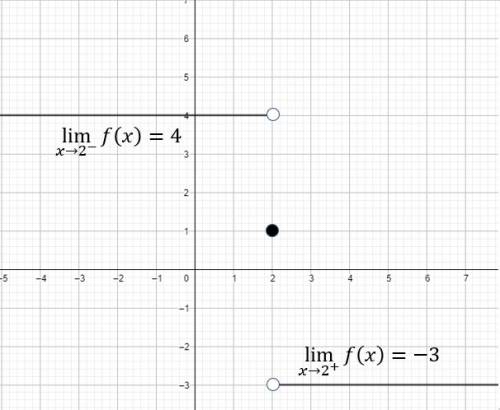
ANSWER TO Q6
The graph that has been described in the question is shown in the diagram above,
We can see from the graph that as we approach 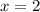 , from the left, the y-values are approaching
, from the left, the y-values are approaching 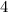 .
.
That is,
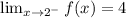
Also as we approach 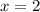 from the right, the y-values are approaching
from the right, the y-values are approaching 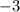 .
.
That is,
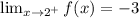 .
.
Ans: D.
ANSWER TO Q7
The given piece-wise function is
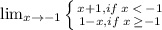
Since 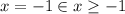
We evaluate the limit at 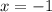 of
of 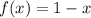 .
.
Since this is a polynomial function, 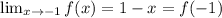
This implies that,
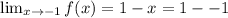
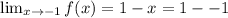
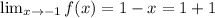
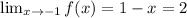
Ans: B.
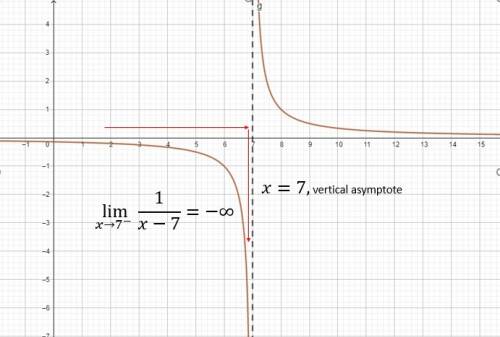
ANSWER TO Q8
The given function is 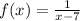 .
.
This is a rational function that is defined for all real values except,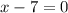
Therefore the vertical asymptote is 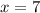
We can see from the graph above that, as x approaches seven from the left, the function approaches negative infinity
That is 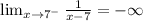 .
.
Ans: A.
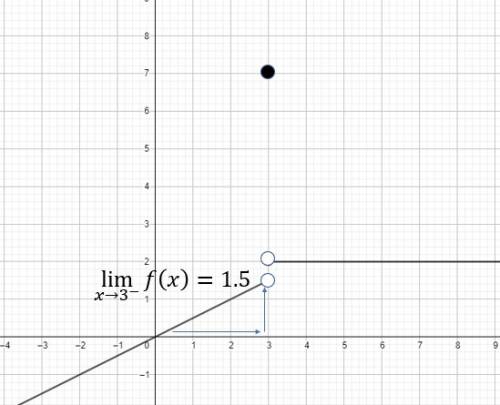
ANSWER TO Q9
The graph of the given piece-wise function is show as follows;
We can see from the graph that, as the x-values are approaching 3 from the left y-values are approaching 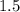 .
.
Note the limit is not the same as the functional value in this case. Also limit in this case is the y-value we are approaching as we get closer and closer to 3, not necessarily at 3.
See graph
Ans: B
ANSWER TO Q10
The given function is 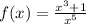
We want to find the limiting value of this function as the x-values approaches zero.
Thus,
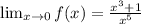
Since the function is not defined at 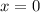 .
.
We evaluate the one-sided limits as follows,
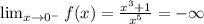
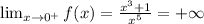
Since the right hand limit is not equal to the left hand limit,
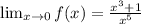 Does Not Exist.
Does Not Exist.
ANS: C
ANSWER TO Q11
The given function is
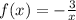
To find the derivative of this function at,
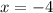 , we must first differentiate this function.
, we must first differentiate this function.
But let us rewrite the rational function as a power function so that it will be easier to differentiate using the power rule of differentiation.
That is,
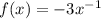 .
.
We differentiate now to obtain,
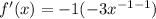
This implies that,
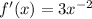
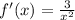
At 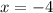
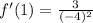
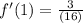
Ans: B
ANSWER TO Q12
We want to find the limit of the function 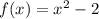 as x approaches zero.
as x approaches zero.
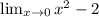
This is a polynomial function, therefore
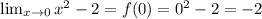
Ans: B
SEE ATTACHMENT FOR ANSWER TO QUESTIONS
13, 14 and 15