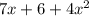Q1 - D. f(x) = 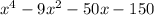
Q13 - A. ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
Q14 - A. 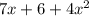
Step-by-step explanation:
Question 1:
We know that rational roots always occurs in pairs. So, the zeros of the function will be 5, -3, -1+3i, -1-3i
So, the factored form is 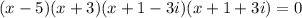
i.e. 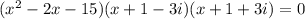
i.e. 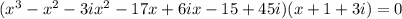
i.e. 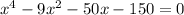
Hence, the polynomial function is 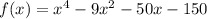 .
.
Question 13:
Rational Zeros Theorem states that 'If p(x) is a polynomial with integer coefficients and if  is a zero of p(x) = 0. Then, p is a factor of the constant term of p(x) and q is a factor of the leading coefficient of p(x)'.
is a zero of p(x) = 0. Then, p is a factor of the constant term of p(x) and q is a factor of the leading coefficient of p(x)'.
Let,  is a zero of
is a zero of 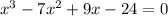 . Then, p is a factor of -24 and q is a factor of 1.
. Then, p is a factor of -24 and q is a factor of 1.
Thus, possible values of p = ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24 and q = ±1
This gives, possible values of  are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
Question 14:
We have, f(x) = 7x + 6 and g(x) = 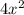
Then, (f+g)(x) = f(x) + g(x) = 7x + 6 + 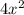
So, (f+g)(x) =