B. z = 2
Step-by-step explanation:
Set up the matrix like this. I multiplied the last row by a 2 to get rid of the fractions so that's what you will see:
![\left[\begin{array}{ccc}2&1&-1\\0&2&3\\-1&2&2\end{array}\right]](/tpl/images/0013/8538/78d55.png)
I used Cramer's Rule to solve for the value of y. In order to do that you need to find the determinant of the matrix, then you need to find the determinant of the matrix after you sub the solution set into the column representing z.
Find the determinant requires that I "pick up" the first 2 columns and then drop them at the end of the matrix and do the multiplication of the majors minus the minors. The matrix looks like this:
2 1 -1 2 1
0 2 3 0 2
-1 2 2 -1 2
The multiplication of the majors:
[(2×2×2)+(1×3×-1)+(-1×0×2)] = (8-3+0)=5
The multiplication of the minors:
[(-1×2×-1)+(2×3×2)+(2×0×1)] = (2+12+0) = 14
So the determinant of the matrix is I A I = 5 - 14 = -9
Now for the determinant of z, noted as I 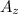 I. Notice that I am replacing the laast column with the solution set this time:
I. Notice that I am replacing the laast column with the solution set this time:
2 1 -8 2 1
0 2 -6 0 2
-1 2 -8 -1 2
The multiplication of the majors:
[(2×2×-8)+(1×-6×-1)+(-8×0×2)] = (-32+6+0) = -26
The multiplication of the minors:
[(-1×2×-8)+(2×-6×2)+(-8×0×1)] = (16 - 24 + 0) = -8
So the determinant of I 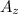 I = -18
I = -18
Cramer's Rule is to divide I 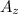 I by I A I:
I by I A I:
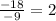
So the value you need for z to solve for y is 2