Find the values of a, b, and c such that the equation y=ax2+bx+c has ordered pair solutions (1,16), (−1,−2), and (0,−1). To do so, substitute each ordered pair solution into the equation. Each time, the result is an equation in three unknowns, a, b, and c. Then solve the resulting system of three linear equations in three unknowns, a, b, and c.

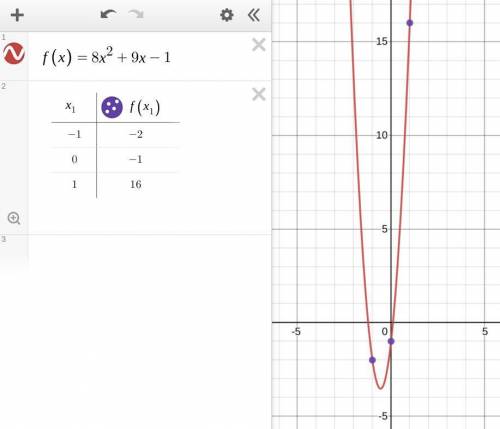
  y = 8x² +9x -1

Step-by-step explanation:

The coefficients of the quadratic function can be found from three points by substituting the point values into the equation and solving for the coefficients.

The equation we want to find coefficients for is ...

  y = ax² +bx +c

For point (1, 16), the equation is 16 = a(1²) +b(1) +c

For point (-1, -2), the equation is -2 = a(-1)² +b(-1) +c

For point (0, -1), the equation is -1 = a(0) +b(0) +c

__

The last of these equations gives a value for c (c=-1). Substituting that into the other two gives the equations in a and b as ...

  a + b = 17

  a - b = -1

Adding the two equations gives ...

  2a = 16   ⇒   a = 8

Subtracting the second from the first gives ...

  2b = 18   ⇒   b = 9

Then the desired quadratic equation is ...

  y = 8x² +9x -1

The answer is in the image 

The answer is in the image 

The answer is in the image 

y=2x+15

where y=Value of coin

x=Age in years

Value of coin after 19 years=2*19+15

=$53

Therefore, Value after 19 years=$53

Here,

tip=18%of $32

tip=(18/100)*32

=0.18*32

=$5.76

Total payment=32+5.76=$37.76

Speed=Distance/time

Here,

distance=15m

time=1sec

speed=15/1=15m/sec

Distance=Speed*time

time=15min=15*60sec=900sec

Distance travelled in 15 min=15*900=13,500m

=13500/1000 km=13.5Km

Salesperson will make 6% of 1800

=(6/100)*1800

=108

Salesperson will make $108 in $1800 sales

The answer is in the image 

The answer is in the image