ANSWER TO QUESTION 1.
We use the Pythagoras Theorem to determine the height of the shelf.
Let
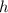
be the height of the triangle,
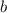
the base and

the hypotenuse.
Then by the Pythagoras Theorem,
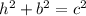
We substitute the base,
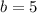
and the hypotenuse

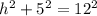
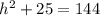
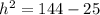
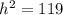
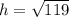
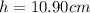
.
Therefore the approximate minimum height of the shelf should be
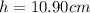
.
the correct answer is A
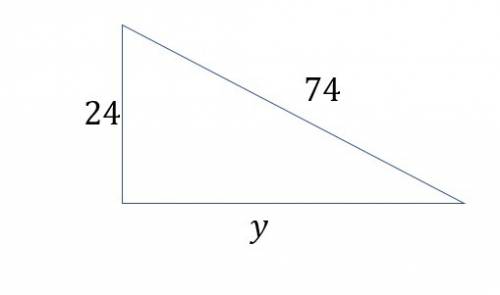
ANSWER TO QUESTION 2
We apply the Pythagoras Theorem to find the length of the third side.
See diagram
Let the length of the third side be
.
Then
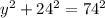
We can now solve for y.
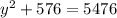
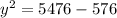
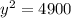
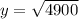
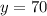
The correct answer is C
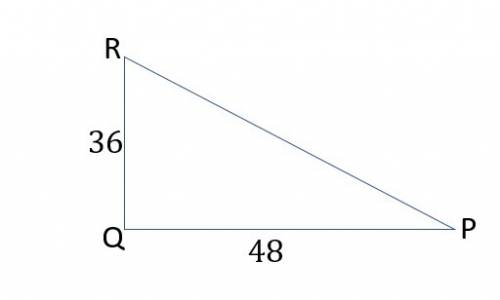
ANSWER TO QUESTION 3
We use the Pythagoras Theorem to find the length of PR.
Since PR is the hypotenuse .
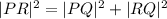
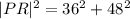
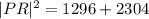
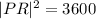
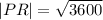
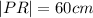
The correct answer is C
See diagram in attachment.
ANSWER TO QUESTION 4
The unknown length is the variable

, which is the hypotenuse of the right angle triangle.
So we use the Pythagoras theorem to find the unknown length.
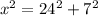
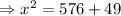
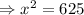
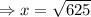
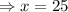
The correct answer is C
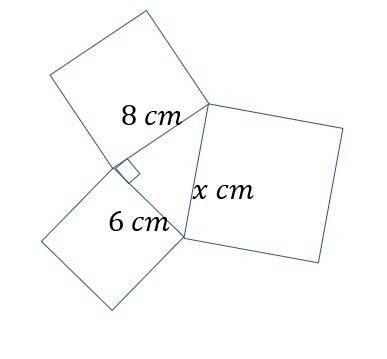
ANSWER TO QUESTION 5.
From Pythagoras Theorem, the area of the bigger square is equal to the area of the two smaller squares added together.
See diagram in attachment.
That is
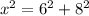
.
This implies that,
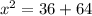
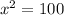
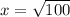
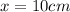
The correct answer is D
ANSWER TO QUESTION 6
Let

be the length of the unknown leg.
Then from the Pythagoras Theorem,
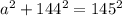
This implies that;
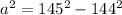
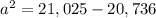
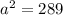
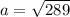
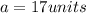
The correct answer is option A.
It is incorrect because the length of the unknown side is
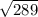
and not
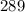
.
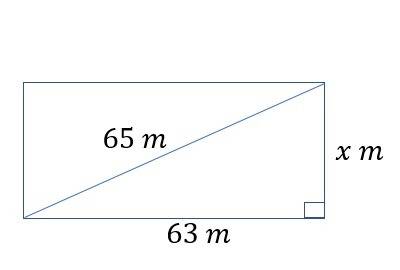
ANSWER TO QUESTION 7
The diagonal is the hypotenuse of the right angle triangle created by the diagonal, the width and the length of the rectangle.
Since the diagonal is the hypotenuse and the two shorter sides are the width and the length of the rectangle, we can apply the Pythagoras Theorem to find the value of

.
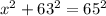
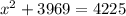
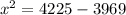
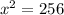
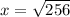
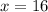
The correct answer is B.
ANSWER TO QUESTION 8
Since the width of the cups is 2 inches, it means the radius is half the width.
That is
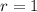
inch
The volume of a cylinder is given by;
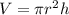
The cup with the cylindrical shape (B) will hold
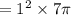
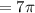
cubic inches of juice
The volume of a cone is:
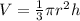
The cup with the conical shape cup(A), will hold
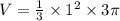
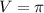
cubic inches of juice
Hence cup B will hold
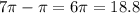
cubic inches than cup A.
The correct answer is A