1) C 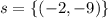 2) (-2,0) 3)
2) (-2,0) 3)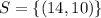 4)
4) 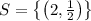 5) c )S={(0,3)} 6) (0,2) 7)
5) c )S={(0,3)} 6) (0,2) 7) 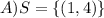 8) Missing graph 9) Vertical line (check below) 10) B 11)
8) Missing graph 9) Vertical line (check below) 10) B 11)
Step-by-step explanation:
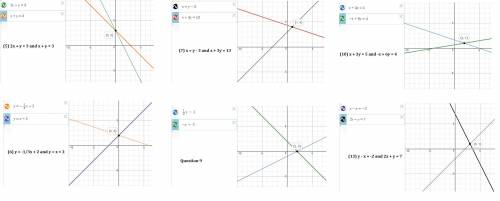
1) Solving by the Addition/Elimination Method. Firstly, let's reduce one variable by making some algebraic adjustments and then adding it up:
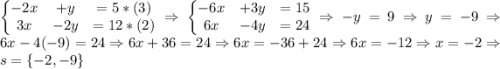
2) Solving by Substitution Method. Where y=x+2 is plugged in the 2nd equation.
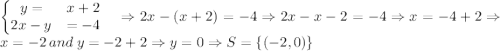
3) Solving it, again, by the Substitution Method due to the I equation form:
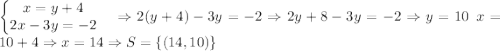
4) By the Addition Method
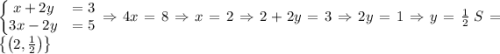
5) To use the graph method to solve the system of Linear equations is possible by graphing each equation on the Cartesian Plane.
Check the graph below, this system has only one solution.
c)S={(0,3)}
6) Solving y=-1/3x+2 y=x+2
(Check the graph below)
A) A) (0, 2)
7) Solving by Substitution Method:
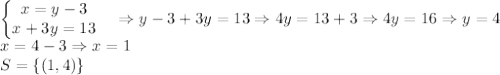
8) Missing graph
9)
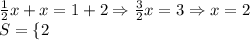
Check the graph below its answer
10) Solving by the Addition Method
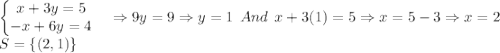
11) Sorry, missing graph for the question.
12) Sorry, missing graph for the question.
13) D Check the graph below
14) Sorry, missing graph for the question.