Part 1)
we know that
the equation of the line in slope-intercept form is equal to
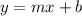
where
m is the slope
b is the y-intercept
we have
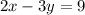
solve for y
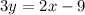
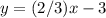 -------> equation of the line in slope-intercept form
-------> equation of the line in slope-intercept form
so
the slope m is 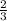
the y-intercept b is 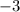
Part 2)
we know that
the equation of the line in slope-intercept form is equal to
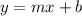
where
m is the slope
b is the y-intercept
we have
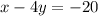
solve for y
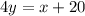
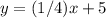 -------> equation of the line in slope-intercept form
-------> equation of the line in slope-intercept form
so
the slope m is 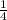
the y-intercept b is 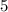
Part 3)
we know that
The x-intercept is the value of x when the value of y is equal to zero
The y-intercept is the value of y when the value of x is equal to zero
we have
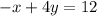
a) Find the x-intercept
For 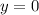 substitute in the equation
substitute in the equation

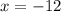
The answer part 3a) is 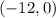
b) Find the y-intercept
For 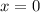 substitute in the equation
substitute in the equation
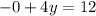
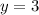
The answer part 3b) is 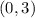
Part 4)
we know that
the equation of the line in standard form is
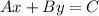
we have
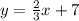
Multiply by 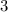 both sides
both sides
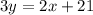
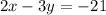 ------> equation in standard form
------> equation in standard form
therefore
the answer Part 4) is option B False
Part 5)
Step 1
Find the slope
we have
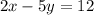
solve for y
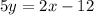
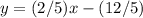
so
the slope m is 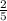
Step 2
Find the y-intercept
The y-intercept is the value of y when the value of x is equal to zero
we have
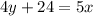
for 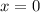
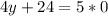
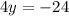
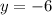
the y-intercept is 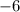
Step 3
Find the equation of the line
we have
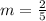
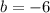
the equation of the line in slope-intercept form is
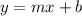
substitute the values
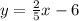
therefore
the answer Part 5) is the option A 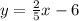
Part 6)
Step 1
Find the slope of the given line
we know that
if two lines are perpendicular. then the product of their slopes is equal to minus one
so
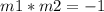
in this problem
the given line
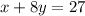
solve for y
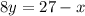
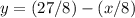
the slope m1 is 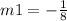
so
the slope m2 is 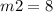
Step 2
Find the equation of the line
we know that
the equation of the line in slope point form is equal to
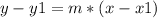
we have
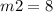
point 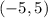
substitutes the values
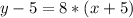
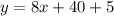
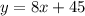
therefore
the answer part 6) is the option C 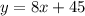
Part 7)
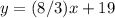 -------> the slope is
-------> the slope is 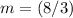
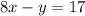
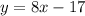 --------> the slope is
--------> the slope is 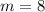
we know that
if two lines are parallel , then their slopes are the same
in this problem the slopes are not the same
therefore
the answer part 7) is the option D) No, since the slopes are different.
Part 8)
a. Write an equation for the line in point-slope form
b. Rewrite the equation in standard form using integers
Step 1
Find the slope of the line
we know that
the slope between two points is equal to
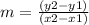
substitute the values
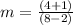
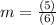
Step 2
Find the equation in point slope form
we know that
the equation of the line in slope point form is equal to
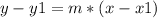
we have
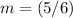
point 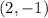
substitutes the values
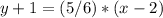 -------> equation of the line in point slope form
-------> equation of the line in point slope form
Step 3
Rewrite the equation in standard form using integers
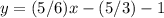
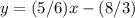
Multiply by 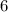 both sides
both sides
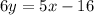
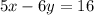 --------> equation of the line in standard form
--------> equation of the line in standard form
Part 9)
we know that
The formula to calculate the slope between two points is equal to
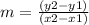
where
(x1,y1) ------> is the first point
(x2,y2) -----> is the second point
In the numerator calculate the difference of the y-coordinates
in the denominator calculate the difference of the x-coordinates
Part 10)
we know that
The formula to calculate the slope between two points is equal to
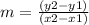
substitutes
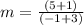
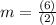
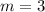
therefore
the answer Part 10) is 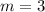
Part 11)
we know that
the equation of the line in slope point form is equal to
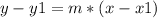
substitute the values
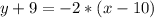 --------> this is the equation in the point slope form
--------> this is the equation in the point slope form