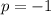Part 1) Option A 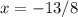
Part 2) Option B 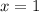
Part 3) Option C 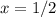
Part 4) Option C 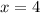
Part 5) Option D 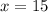
Part 6) Option B 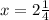
Part 10) Option B 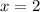
Part 11) Option A 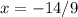
Part 13) Option A 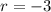
Part 14) Option D
Part 15) Option D
Part 16) Option C 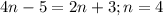
Part 17) Option D 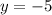
Part 18) Option D 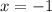
Part 19) Option D distribute the 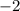 to the
to the 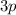 and
and  ; distribute the
; distribute the 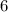 to the
to the 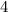 and
and 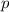
Part 20) Option B 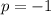
Step-by-step explanation:
Part 1) we have
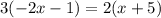
solve for x
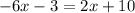
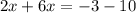

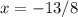
Part 2) we have
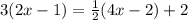
solve for x
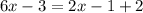
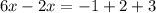
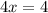
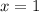
Part 3) we have
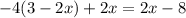
solve for x
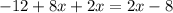
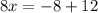
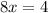
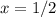
Part 4) we have
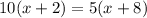
solve for x
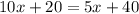
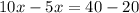
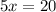
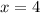
Part 5) we have
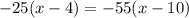
solve for x
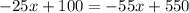
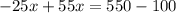
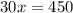
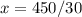
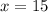
Part 6) we have
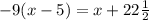
solve for x
remember that
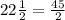
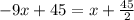
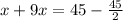
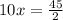
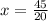
convert to mixed number
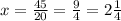
Part 7) The model is not included
Part 8) The model is not included
Part 9) The model is not included
Part 10) we have
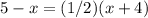
solve for x
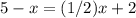
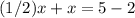
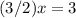
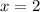
Part 11) we have
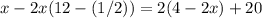
solve for x
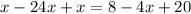
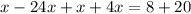
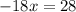
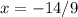
Part 12) The model is not included
Part 13) we have
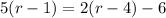
solve for r
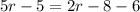

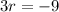
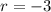
Part 14) and Part 15)
the answer is the option D
Look for parenthesis and apply the distributive property; combine like terms; move your variable terms to one side and constants to the other side of the equal sign; go in reverse PEMorDAorS to isolate the variable using inverse operations
Part 16)
Let
n------> the number
we know that
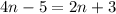 -----> algebraic expression that represent the situation
-----> algebraic expression that represent the situation
solve for n
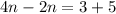
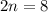
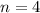
Part 17) we have
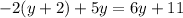
solve for y
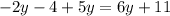
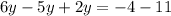
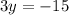
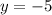
Part 18) we have
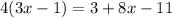
solve for x
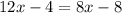
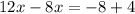
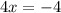
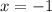
Part 19) we have
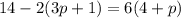
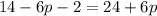 ------> distribute the
------> distribute the 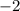 to the
to the 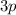 and
and  ; distribute the
; distribute the 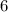 to the
to the 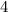 and
and 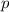
Part 20) we have
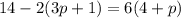
step 1
distribute the 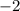 to the
to the 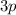 and
and  ; distribute the
; distribute the 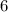 to the
to the 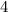 and
and 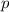
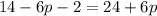
step 2
Group terms that contain the same variable and move the constant to the other side
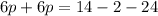
step 3
Combine like terms
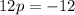
step 4
Divide by 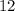 both sides
both sides