Hello, I need help with this. any help is appreciated :)

50 000 cm2 = ? m2

or 5m2

Step-by-step explanation:

1 meter^2 = 10000 cm

There for we could set up a ratio for this problem

Using cross-multiplication we get:

Divide 50,000 by 10000 we get:

Therefore the answer is

50 000 cm2 = 5 m2

Hope this helps! :)

nice i watched HxH

Explanation:

watch assassination classroom or code geass or my hero academia

nice i watched HxH

Explanation:

watch assassination classroom or code geass or my hero academia

Find slope intercept form

Step-by-step explanation:

When you have 2 points, you can find the slope of the line.

Use the y-intercept as a point like (0, y) and the given point (4, 90) to find the slope.

Using this:

Knowing that y=mx+b, plug in either set of points and the slope as m to find b.

Or, because you are already given the y-intercept and b is the y-intercept, fill in b with that y coordinate.

Now rewrite in slope intercept form (y= mx+b), fill in m and b, and you're done!

A. 24

Step-by-step explanation:

We know that the formula for find the area of right triangle is (1/2) × (b × h)

Using this formula, we can find the area of this right triangle given the side lengths

the base of this right triangle is 8

the height of this right triangle is 6

(1/2) × (8×6)

(1/2) × (48)

48/2

24

x = √17 and x = -√17

Step-by-step explanation:

We have the equation:

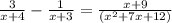
To solve this we need to remove the denominators.

Then we can first multiply both sides by (x + 4) to get:

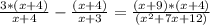
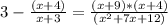
Now we can multiply both sides by (x + 3)

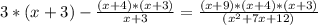
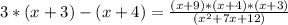
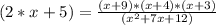
Now we can multiply both sides by (x^2 + 7*x + 12)

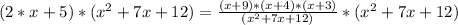
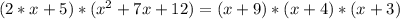
Now we need to solve this:

we will get

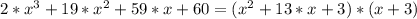
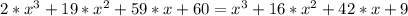
Then we get:

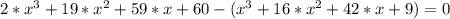
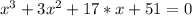
So now we only need to solve this.

We can see that the constant is 51.

Then one root will be a factor of 51.

The factors of -51 are:

-3 and -17

Let's try -3

p( -3) = (-3)^3 + 3*(-3)^2 + +17*(-3) + 51 = 0

Then x = -3 is one solution of the equation.

But if we look at the original equation, x = -3 will lead to a zero in one denominator, then this solution can be ignored.

This means that we can take a factor (x + 3) out, so we can rewrite our equation as:

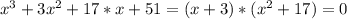
The other two solutions are when the other term is equal to zero.

Then the other two solutions are given by:

x = ±√17

And neither of these have problems in the denominators, so we can conclude that the solutions are:

x = √17 and x = -√17

A. 24

Step-by-step explanation:

We know that the formula for find the area of right triangle is (1/2) × (b × h)

Using this formula, we can find the area of this right triangle given the side lengths

the base of this right triangle is 8

the height of this right triangle is 6

(1/2) × (8×6)

(1/2) × (48)

48/2

24