Linear equations are represented by straight lines.
Graphs
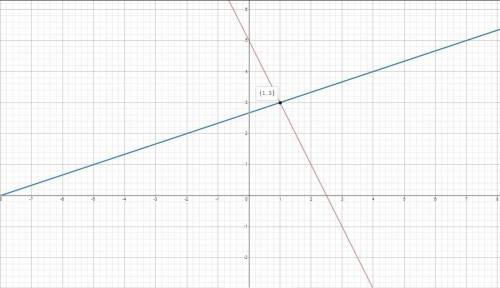
(1) 2x + y = 5 and x - 3y = -8
See attachment for the graphs of 2x + y = 5 and x - 3y = -8
From the graph, we have:
(x,y) = (1,3)
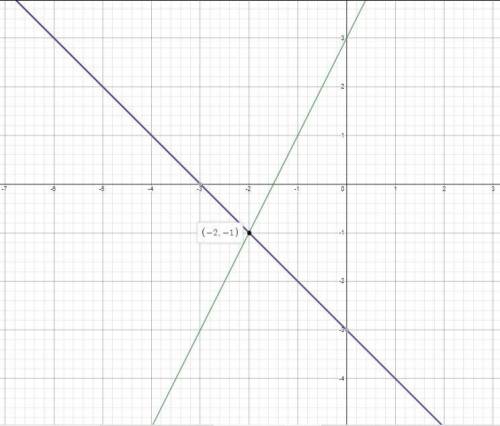
(2) 6x - 3y = -9 and 2x + 2y = -6
See attachment for the graphs of 6x - 3y = -9 and 2x + 2y = -6
From the graph, we have:
(x,y) = (-2,-1)
Substitution
3) y = 5x-3 and -x - 5y = - 11
Make x the subject in 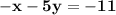
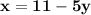
Substitute 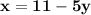 in
in 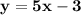
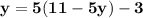
Open bracket
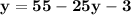
Collect like terms
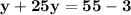
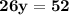
Divide both sides by 2
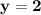
Substitute 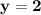 in
in 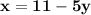
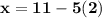
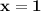
So, the solution is (x,y) = (1,2)
4) 2x - 6y = 24 and x - 5y = 22
Make x the subject in 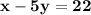
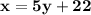
Substitute 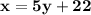 in
in 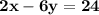
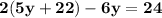
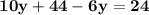
Collect like terms
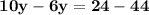
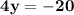
Divide by 4
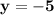
Substitute 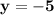 in
in 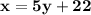
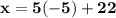
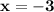
So, the solution is (x,y) = (-3,-5)
Elimination
5) - 4x - 2y = -2 and 4x + 8y = -24
Add both equations to eliminate x
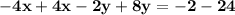
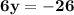
Divide both sides by 6
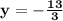
Substitute 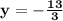 in
in 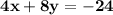
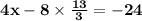
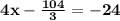
Collect like terms
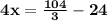
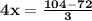
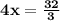
Divide both sides by 4
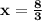
Hence, the solution is (x,y) = (8/3,-13/3)
6) x - y = 11 and 2x + y = 19
Add both equations to eliminate y
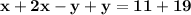
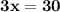
Divide through by 3
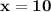
Substitute 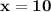 in
in 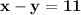
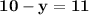
Collect like terms
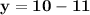
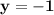
Hence, the solution is (x,y) = (10,-1)
Read more about linear equations at:
link