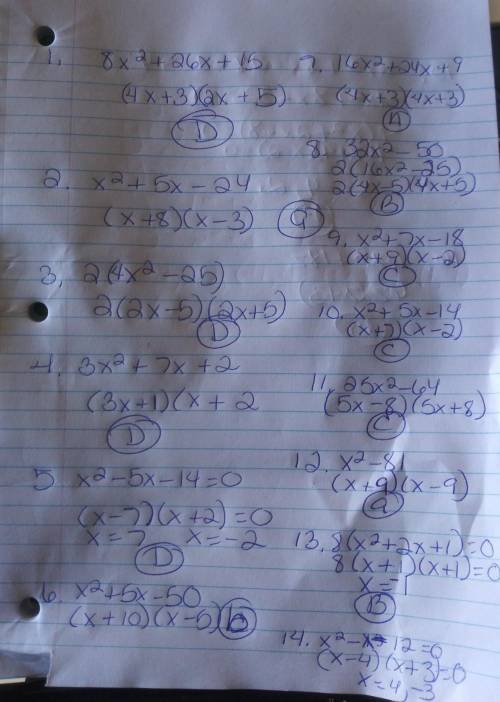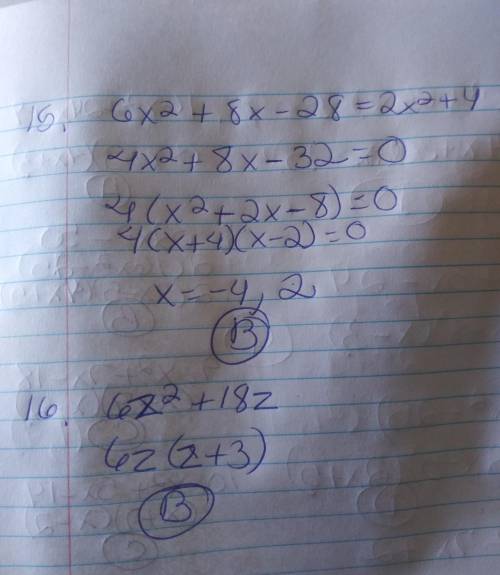Following are the calculation to the given points:
For point 1:
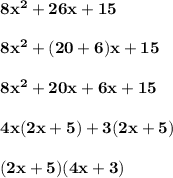
Therefore, the answer is "Option D".
For point 2:
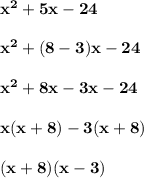
Therefore, the answer is "Option A".
For point 3:
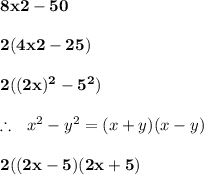
Therefore, the answer is "Option D".
For point 4:
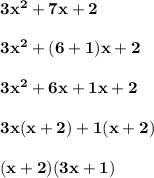
Therefore, the answer is "Option D".
For point 5:
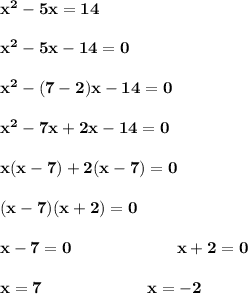
Therefore, the answer is "Option D".
For point 6:
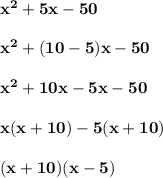
Therefore, the answer is "Option B".
For point 7:
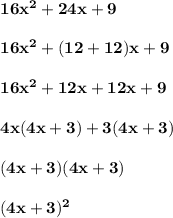
Therefore, the answer is "Option A".
For point 8:
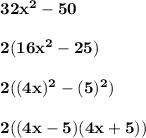
Therefore, the answer is "Option B".
For point 9:
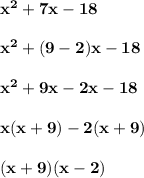
Therefore, the answer is "Option C".
For point 10:
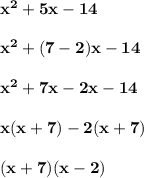
Therefore, the answer is "Option C".
For point 11:
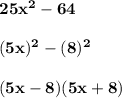
Therefore, the answer is "Option C".
For point 12:
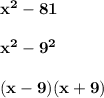
Therefore, the answer is "Option A".
For point 13:
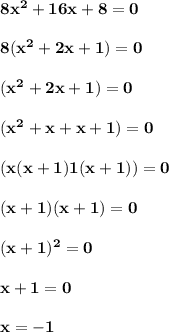
Therefore, the answer is "Option B".
For point 14:
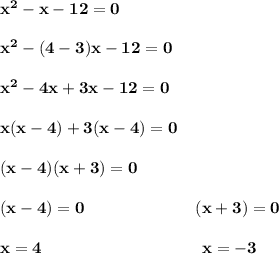
Therefore, the answer is "Option C".
For point 15:
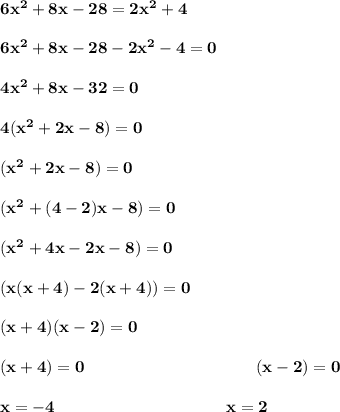
Therefore, the answer is "Option B".
For point 14:
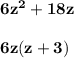
Therefore, the answer is "Option B".
Learn more:
link