If 15% of sum is Rs 45, find the sum., №18011025, 11.02.2021 09:16

Mathematics

Step-by-step answer

P Answered by Specialist

answer : the sum so obtained is rupees 300

StudenGPT

2.2. In a class investigation, the heights of Grade 8 learners were measured and inverted he measurements to the nearest centimetre. The measurements are as follows: begin{tabular}{|l|l|l|l|l|l|l|} hline 140 & 138 & 142 & 144 & 148 & 145 & 152 hline 141 & 138 & 144 & 144 & 148 & 146 & 153 hline 141 & 139 & 144 & 144 & 150 & 146 & 154 hline 142 & 139 & 143 & 144 & 150 & 147 & 155 hline 142 & 140 & 144 & 145 & 151 & 148 & 156 hline

Step-by-step answer

P Answered by Studen AI

2.2.1. Would you classify this data as quantitative or qualitative? Explain your answer.

This dataset is quantitative because it consists of numerical values (heights of the students). Quantitative data can be measured and can be used in calculations and statistical analyses.

2.2.2. Is the data discrete or continuous? Explain your answer.

The data is discrete because the heights are specific values measured to the nearest centimetre. If the data were measured to an extremely precise degree (like if we had an infinite number of possible measurements), it would be continuous.

2.2.3. Employ GeoGebra to summarize the data using a stem and leaf plot.

Unfortunately, as I am a text-based AI, I can't create a stem and leaf plot using GeoGebra. However, I can explain how to do it.

Firstly, you would organize the data from least to greatest. Identify the 'stem' (the first digits, e.g., for numbers like 141, 142, the stem will be 14) and the 'leaf' (the last digit, e.g., 1 and 2 for the numbers 141 and 142, respectively).

Once you have stems and leaves identified, use GeoGebra to plot the data. You will have a vertical column for stems (representing the value in the tens place) and horizontal rows for leaves (representing the values in the ones place).

2.2.4. Analyse the data you organized in 2.2.3 by writing three statements.

As I lack the visual presentation, I will assume you organized and plotted the data correctly in the stem and leaf plot. Some possible statements could be:

1. The majority of the students' heights are in the 140-149 cm range.
2. There are few students with heights below 140 cm or above 150 cm.
3. The greatest number of students have height 144 cm.

2.2.5. You want to introduce the concept of intervals to the Grade 8 learners. How would you explain the term "interval" using the ordered stem-and-leaf plot you plotted in 2.2.3 as an example?

An interval is a set of real numbers that lies between two numbers, the endpoints. In the context of our stem-and-leaf plot, the values on the stem could be considered intervals - for instance, the 140s represent an interval that includes all heights from 140 to 149 cm.

Each student's height that falls within this range is a data point within this interval. So, we can say that students' heights are spaced at discrete intervals, depending on the tens place of each height measurement. Intervals help to group and visualize data in a convenient and efficient manner.

Remember to follow these steps meticulously and ensure accuracy in all your calculations. Always double-check for correctness.

Mathematics

Based on the data in the two-way table, which statement is true? a. p(consumes 1,000−1,500 calories|weight is 165) = p(consumes 1,000−1,500 calories) b. p(weight is 120 lb.|consumes 2,000−2,500 calories) ≠ p(weight is 120 lb.) c. p(weight is 165 lb.|consumes 1,000−2,000 calories) = p(weight is 165 lb.) d. p(weight is 145 lb.|consumes 1,000−2,000 calories) = p(consumes 1,000−2,000 calories) weight/calories per day: 120 145 160/total 1000 to 1500 cal: 90 35 15/total 140 1500 to 2000 cal: 80 143 27/total 250 2000 to 2500 cal: 10 25 75/total 110 total:

Step-by-step answer

P Answered by Specialist

64

B. P(weight is 120 lb.|consumes 2,000−2,500 calories) ≠ P(weight is 120 lb.)

Step-by-step explanation:

The probability that a person consumes between 1000 and 1500 calories given that the person weighs 165 is found by first finding the number of people weighing 165 that consume between 1000 and 1500 calories. There are 15 people in that category. The probability will be out of the total number of people that weigh 165; this is 117. This makes the probability 15/117 = 0.128.

The probability that someone consumes between 1000 and 1500 calories is given by first finding the number of people that consume that many calories. This number is 140. The probability will be out of the total number of people; this is 500. This makes the probability 140/500 = 0.28.

Since these are not the same, A is not true.

The probability that someone weighs 120 given that they consume between 2000 and 2500 calories is found by first finding the number of people weighing 120 that consume between 2000 and 2500 calories. There are 10 people in that category. The probability will be out of the total number of people that consume between 2000 and 2500 calories; this is 110. This makes the probability 10/110 = 0.09.

The probability that someone weighs 120 pounds is given by first finding the number of people that weigh 120 pounds. This is 180. The probability will be out of the total number of people; this is 500. This makes the probability 180/500 = 0.36.

Since these are not the same, B is true.

The probability that someone weighs 165 given that they consume between 1000 and 2000 calories is found by first finding the number of people weighing 165 that consume between 1000 and 2000 calories. There are 15+27 = 42 people in that category. The probability will be out of the total number of people that consume between 1000 and 2000 calories; this is 140+250 = 390. This makes the probability 42/390 = 0.108.

The probability that someone weighs 165 pounds is given by first finding the number of people that weigh 165 pounds. This is 117. The probability will be out of the total number of people; this is 500. This makes the probability 117/500 = 0.234.

Since these are not the same, C is not true.

The probability that someone weighs 145 given that they consume between 1000 and 2000 calories is found by first finding the number of people weighing 145 that consume between 1000 and 2000 calories. There are 35+143 = 178 people in that category. The probability will be out of the total number of people that consume between 1000 and 2000 calories; this is 140+250 = 390. This makes the probability 178/390 = 0.456.

The probability that someone consumes between 1000 and 2000 calories is given by first finding the number of people that consume between 1000 and 2000 calories. This is 140+250 = 390. The probability will be out of the total number of people; this is 500. This makes the probability 390/500 = 0.78.

Since these are not the same, D is not true.

Mathematics

Based on the data in the two-way table, which statement is true? a. p(consumes 1,000−1,500 calories|weight is 165) = p(consumes 1,000−1,500 calories) b. p(weight is 120 lb.|consumes 2,000−2,500 calories) ≠ p(weight is 120 lb.) c. p(weight is 165 lb.|consumes 1,000−2,000 calories) = p(weight is 165 lb.) d. p(weight is 145 lb.|consumes 1,000−2,000 calories) = p(consumes 1,000−2,000 calories) weight/calories per day: 120 145 160/total 1000 to 1500 cal: 90 35 15/total 140 1500 to 2000 cal: 80 143 27/total 250 2000 to 2500 cal: 10 25 75/total 110 total:

Step-by-step answer

P Answered by Specialist

64

B. P(weight is 120 lb.|consumes 2,000−2,500 calories) ≠ P(weight is 120 lb.)

Step-by-step explanation:

The probability that a person consumes between 1000 and 1500 calories given that the person weighs 165 is found by first finding the number of people weighing 165 that consume between 1000 and 1500 calories. There are 15 people in that category. The probability will be out of the total number of people that weigh 165; this is 117. This makes the probability 15/117 = 0.128.

The probability that someone consumes between 1000 and 1500 calories is given by first finding the number of people that consume that many calories. This number is 140. The probability will be out of the total number of people; this is 500. This makes the probability 140/500 = 0.28.

Since these are not the same, A is not true.

The probability that someone weighs 120 given that they consume between 2000 and 2500 calories is found by first finding the number of people weighing 120 that consume between 2000 and 2500 calories. There are 10 people in that category. The probability will be out of the total number of people that consume between 2000 and 2500 calories; this is 110. This makes the probability 10/110 = 0.09.

The probability that someone weighs 120 pounds is given by first finding the number of people that weigh 120 pounds. This is 180. The probability will be out of the total number of people; this is 500. This makes the probability 180/500 = 0.36.

Since these are not the same, B is true.

The probability that someone weighs 165 given that they consume between 1000 and 2000 calories is found by first finding the number of people weighing 165 that consume between 1000 and 2000 calories. There are 15+27 = 42 people in that category. The probability will be out of the total number of people that consume between 1000 and 2000 calories; this is 140+250 = 390. This makes the probability 42/390 = 0.108.

The probability that someone weighs 165 pounds is given by first finding the number of people that weigh 165 pounds. This is 117. The probability will be out of the total number of people; this is 500. This makes the probability 117/500 = 0.234.

Since these are not the same, C is not true.

The probability that someone weighs 145 given that they consume between 1000 and 2000 calories is found by first finding the number of people weighing 145 that consume between 1000 and 2000 calories. There are 35+143 = 178 people in that category. The probability will be out of the total number of people that consume between 1000 and 2000 calories; this is 140+250 = 390. This makes the probability 178/390 = 0.456.

The probability that someone consumes between 1000 and 2000 calories is given by first finding the number of people that consume between 1000 and 2000 calories. This is 140+250 = 390. The probability will be out of the total number of people; this is 500. This makes the probability 390/500 = 0.78.

Since these are not the same, D is not true.

Mathematics

15and explain how to solve i really want to understand it karl opens a savings account with $2500. he deposits $1500 every year into the account that has a 0.75% interest rate, compounded monthly. if he doesn’t withdraw any money, what will the account balance be in 10 years? $15,581.51 $15,571.78 $18,276.16 $18,266.43 sophia knows that she needs $42,000 for a 20% down payment on a house she can afford. she found an investment that earns 2.25% interest compounding monthly. how much should she put in the account now, rounded to the nearest dollar,

Step-by-step answer

P Answered by Specialist

19

1) idk I got none of your options
2)p=42,000÷(1+0.0225÷12)^(12×5)
P=37,535.04
3)PVAO=4900*12[(1/0.029)-(1/0.029*(1+0.029)^10]=504145.41..compare with 500000
So the answer is D
4)lucas
90×87.92=7,912.8
((8,476.20−7,912.8)
÷7,912.8)×100=7.1%
Peton
55×72.03=3,961.65
((4,192.10−3,961.65)
÷3,961.65)×100=5.8%
So the answer is D

Mathematics

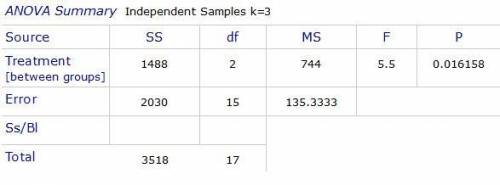
The following data are from a completely randomized design. Treatment A B C 162 142 126 142 156 122 165 124 138 145 142 140 148 136 150 174 152 128 Sample mean 156 142 134 Sample variance 164.4 131.2 110. a. Compute the sum of squares between treatments. b. Compute the mean square between treatments. c. Compute the sum of squares due to error. d. Compute the mean square due to error. e. Set up the ANOVA table for this problem. f. At the α = . 05 level of significance, test whether the means for the three treatments are equal.

Step-by-step answer

P Answered by Master

a)1488

b) 744

c) 2030

d) 135.333

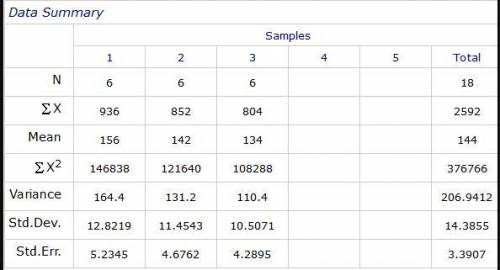
e) see attached table

f) There is sufficient evidence to reject the claim of equal means.

Step-by-step explanation:

a) Determine the value of total-group variability SS(tot):

SS(tot)=∑x^2(tot)-(x(tot))^2/N=376766-2592^2/18 ≅ 3518

Determine the value of the sum of squares between groups:

SS(bet) = ∑_(all groups) (∑x_i)^2/n_i -(∑x(tot))^2/N

=936^2/6+852^2/6+804^2/6-2592^2/6≅ 1488

b) d.f(BET) is the number of groups k decreased by 1.

d.f(BET) = k - 1= 3-1 = 2

MS(BET) is SS(BET) divided by d.f(BET):

MS(BET)=SS(BET)/ d.f(BET)

=1488/2

=744

c) The value of the sum of squares within groups (due to error) is then the value of the total-group variability decreased by the value of the sum of squares between groups (Note: using this calculation you then immediately obtain that the sum SS(tot) =SS(bet)+ SS(W) holds):

SS(W) = SS(tot) - SS(bet) = 3518 - 1488 = 2030

d) d.f.w is the total sample size decreased by the number of groups k.

d.f.w = N — k = 18 — 3 = 15

MSw is SSw divided by d.f.w:

MSw =SSw/d.f.w=2030/15=135.333

e) see attached table

f) The value of the test statistic F is then MS(BET) divided by MSw:

F=MS(BET)/MSw=744/135.3333≅5.5

The degrees of freedom are the same as those for between groups and within groups:

d.f.N=d.f(BET)=2

d.f.D=d.f.w=15

The P-value is the probability of obtaining the value of the test statistic, or a value more extreme. The P-value is the number (or interval) in the column title of Table 4 containing the F-value in the row dfn = 2 and dfd = 15:

0.01<P<0.025

If the P-value is less than the significance level, reject the null hypothesis.

P<0.05==> Reject H_o

There is sufficient evidence to reject the claim of equal means.

The following data are from a completely randomized design. Treatment A B C 162 142 126 142 156 122

Mathematics

15and explain how to solve i really want to understand it karl opens a savings account with $2500. he deposits $1500 every year into the account that has a 0.75% interest rate, compounded monthly. if he doesn’t withdraw any money, what will the account balance be in 10 years? $15,581.51 $15,571.78 $18,276.16 $18,266.43 sophia knows that she needs $42,000 for a 20% down payment on a house she can afford. she found an investment that earns 2.25% interest compounding monthly. how much should she put in the account now, rounded to the nearest dollar,

Step-by-step answer

P Answered by Master

19

1) idk I got none of your options
2)p=42,000÷(1+0.0225÷12)^(12×5)
P=37,535.04
3)PVAO=4900*12[(1/0.029)-(1/0.029*(1+0.029)^10]=504145.41..compare with 500000
So the answer is D
4)lucas
90×87.92=7,912.8
((8,476.20−7,912.8)
÷7,912.8)×100=7.1%
Peton
55×72.03=3,961.65
((4,192.10−3,961.65)
÷3,961.65)×100=5.8%
So the answer is D

Mathematics

A study is performed in a large southern town to determine whether the average amount spent on food per four-person family in the town is significantly different from the national average. A random sample of the weekly grocery bills of two-person families in this town is given in the file. Assume the national average amount spent on food for a four-person family is $150. a. Identify the null and alternative hypotheses for this situation. b. Is the sample evidence statistically significant? If so, at what significance levels can you reject the null

Step-by-step answer

P Answered by PhD

Step-by-step explanation:

H0: u = 150

H1: u ≠ 150

Total sum = 15933.24

N = 100

Mean = 15933.24/100

= 159.3324

σ² = 25954.03 - (159.3324)²/100

σ² = 556.213

σ = √556.213

σ = 23.8162

Testing hypothesis

t = (bar x - u)/ σ/√n

= 159.3324-150/23.8162/√100

= 3.91

We will have a p value of 0.02

0.0002 < 0.01

We reject null hypothesis at 1% level of significance

C. Mean = 159.3324

Se= 2.3936

Df = 100-1 = 99

Critical value at 0.01 = +-2.626

T = x-u/s.e

= -2.626 =( x -150)/2.3936

When we cross multiply and solve this

X = 143.714 for the lower tail

2.626 = (x-159)/2.3936

= 156.286 for upper tail.

We therefore reject H0 at

Bar X <= 143.71

Bar X >= 156.286

At 10%

Critical t = 1.660

-1.660 = (x - 150)/2.3936

Solving this ,

X =146.02 at the lower tail

1.660 = (x-150)/2.3936

X = 153.97

We reject H0 at

X<= 146.03

X>=153.97

Business

Billions of Dollars Investment 80 Capital consumption allowance (depreciation) 45 Exports 40 Imports 15 Government purchases 160 Consumption 375 Indirect business taxes 35 Social insurance taxes 5 Corporate profit taxes 4 Undistributed corporate profits 6 Transfer payments 50 Personal taxes 110 Compensation of employees 455 Corporate profits 90 Rental income (of persons) 5 Net interest 25 Proprietors income 25 Income earned from the rest of the world 80 Income earned by the rest of the world 40 The five components of GDP from the table that together

Step-by-step answer

P Answered by Master

Note: Some words are missing and are attached as picture below

The 5 components of GDP from the table that together sum to national income are:

a. Compensation of employees

b. Corporate profits

c. Net interest

d. Proprietors' income

e. Rental income

Disposable Income = Personal Income - Personal Taxes

Personal Income = Disposable Income + Personal Taxes

Personal Income = 525 + 110

Personal Income = 635

National income = Personal Income + Social Insurance Tax + Corporate Profit Taxes + Undistributed Corporate Profits - Transfer Payments

National income = 635 + 5 + 4 + 6 - 50

National income = 600

Billions of Dollars

Investment 80
Capital consumption allowance (depreciation) 45
Exports 40
Imp

Mathematics

A study is performed in a large southern town to determine whether the average amount spent on food per four-person family in the town is significantly different from the national average. A random sample of the weekly grocery bills of two-person families in this town is given in the file. Assume the national average amount spent on food for a four-person family is $150. a. Identify the null and alternative hypotheses for this situation. b. Is the sample evidence statistically significant? If so, at what significance levels can you reject the null

Step-by-step answer

P Answered by PhD

Step-by-step explanation:

H0: u = 150

H1: u ≠ 150

Total sum = 15933.24

N = 100

Mean = 15933.24/100

= 159.3324

σ² = 25954.03 - (159.3324)²/100

σ² = 556.213

σ = √556.213

σ = 23.8162

Testing hypothesis

t = (bar x - u)/ σ/√n

= 159.3324-150/23.8162/√100

= 3.91

We will have a p value of 0.02

0.0002 < 0.01

We reject null hypothesis at 1% level of significance

C. Mean = 159.3324

Se= 2.3936

Df = 100-1 = 99

Critical value at 0.01 = +-2.626

T = x-u/s.e

= -2.626 =( x -150)/2.3936

When we cross multiply and solve this

X = 143.714 for the lower tail

2.626 = (x-159)/2.3936

= 156.286 for upper tail.

We therefore reject H0 at

Bar X <= 143.71

Bar X >= 156.286

At 10%

Critical t = 1.660

-1.660 = (x - 150)/2.3936

Solving this ,

X =146.02 at the lower tail

1.660 = (x-150)/2.3936

X = 153.97

We reject H0 at

X<= 146.03

X>=153.97

If 15% of sum is Rs 45, find the sum.

Step-by-step answer

Faq

Try asking the Studen AI a question.