The side lengths of a triangle are 10,26 and, №18011039, 05.03.2020 04:23

Mathematics

The side lengths of a triangle are 10,26 and 24 which one is the hypotenuse a.24 b.26 c.10 d.50

Step-by-step answer

P Answered by Specialist

$\huge\boxed{\bf\: b. \: 26 \rightarrow hypotenuse }$

Step-by-step explanation:

Consider a right angled triangle with sides as 10, 26 & 24 units.

Here, we need to find the hypotenuse of the triangle.

The hyptenuse is the side which is opposite to the right angle (90°) & is also the longest side of the triangle.

Then, among the given values, we can clearly say that 26 > 10, 24.

Therefore, 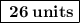$\boxed{\bf\: 26 \: units }$ is the hypotenuse of the triangle with side lengths as 10, 26, 24 units.

$\rule{150pt}{2pt}$

Mathematics

Tell whether the triangle with the given side lengths is a right triangle. 10in., 24in., 26in.

Step-by-step answer

P Answered by Master

1

Answer- Yes it is a right triangle.
You can use the Pythagorean Theorem.
( a^2 + b^ = c^2 ) and replace a with 10, b with 24, and c with 26 and the equation will be balanced on both sides.

(10^2 + 24^2 = 26^2)
(100 + 576 = 676 )

Mathematics

Tell whether the triangle with the given side lengths is a right triangle. 10in., 24in., 26in.

Step-by-step answer

P Answered by Master

1

Answer- Yes it is a right triangle.
You can use the Pythagorean Theorem.
( a^2 + b^ = c^2 ) and replace a with 10, b with 24, and c with 26 and the equation will be balanced on both sides.

(10^2 + 24^2 = 26^2)
(100 + 576 = 676 )

Mathematics

Statistics: the central limit theorem 50 points! 1. when designing motorcycle helmets, the breadth of a person s head must be considered. men have head breadths that are normally distributed with a mean of 6.0 inches and a standard deviation of 1.0 inches. if one male is randomly selected, what is the probability that his head breadth is less than 6.2 inches? a. 0.5793 b. 0.4207 c. 0.2 d. 0.8078 2. for women aged 18-24, systolic blood pressures (in mm hg) are normally distributed with a mean of 114.8 and a standard deviation of 13.1. if 4 women

Step-by-step answer

P Answered by Specialist

17

Your answers are correct. Good Job and have an awesome day!

Mathematics

Need here : ) 5.02 1. solve the triangle. a = 50°, b = 13, c = 6 (2 points) a) a ≈ 10.2, c ≈ 26.3, b ≈ 103.7 b) a ≈ 14, c ≈ 26.3, b ≈ 103.7 c) no triangles possible d) a ≈ 14, c ≈ 30.3, b ≈ 99.7 2. solve the triangle. a = 12, b = 22, c = 95° (2 points) a) c ≈ 26, a ≈ 27.6°, b ≈ 57.4° b) c ≈ 26, a ≈ 54.4°, b ≈ 30.6° c) c ≈ 25.1, a ≈ 27.6°, b ≈ 57.4° d) c ≈ 25.1, a ≈ 31.6°, b ≈ 53.4° 3. find the area of the triangle with the given measurements. round the solution to the nearest hundredth if necessary. a = 50°, b = 30 ft, c = 14 ft (2 points) a) 160.87

Step-by-step answer

P Answered by Master

30

1. A.Use law of cosines. cosA=(b^2+c^2-a^2)/(2bc) because A is the included angle between b and c. Plug in A=50 degrees, b=13, c=6. cos50=(13^2+6^2-a^2)/(2*13*6), a^2=104.7,a=10.2 approximately, so choose A.

2. A.Use law of cosines again. cosC=(a^2+b^2-c^2)/(2ab). C=95 degrees, a=12, b=22. Plug in, cos95=(12^2+22^2-c^2)/(2*12*22), solve the equation, c^2=674, c=26 approximately. The use law of sines to solve for angle A (also works for B), a/sinA=c/sinC, 12/sinA=26/sin95, sinA=0.46, A=arcsin(0.46)=27.6. Choose A.

3. Answer is A. Area=1/2bc*sinA, since A is the included angle between b and c. Plug in b=30, c=14, A=50 degrees, area=1/2*14*30*sin50=160. 87, so the answer is A.

4. D. As long as the sum of any two sides of the triangle is bigger than the third, the triangle exists. 240+121>263, 240+263>121, 263+121>240, so it exists. To use Heron's formula, first find the semiperimeter, (240+263+121)/2=312. A=\sqrt(312*(312-240)*(312-263)*(312-121))=14499.7 approximately, so choose D.

5. 300. The included angle between the two paths is C=49.17+90=139.17 degrees. The lengths of the two paths are a=150, b=170. c is the distance we want. Use the law of cosines, cosC=(a^2+b^2-c^2)/(2ab). Plug in, c^2=89989, c=300 approximately.

Mathematics

Statistics: the central limit theorem 50 points! 1. when designing motorcycle helmets, the breadth of a person s head must be considered. men have head breadths that are normally distributed with a mean of 6.0 inches and a standard deviation of 1.0 inches. if one male is randomly selected, what is the probability that his head breadth is less than 6.2 inches? a. 0.5793 b. 0.4207 c. 0.2 d. 0.8078 2. for women aged 18-24, systolic blood pressures (in mm hg) are normally distributed with a mean of 114.8 and a standard deviation of 13.1. if 4 women

Step-by-step answer

P Answered by Master

17

Your answers are correct. Good Job and have an awesome day!

Mathematics

Which of the following sets of possible side lengths forms a triangle? 6, 9, and 15 4, 10, and 15 10, 15, and 25 12, 12, and 23 which of the following sets of possible side lengths forms a right triangle? 12, 35, and 3811, 60, and 619, 40, and 456, 12, and 13 which of the following sets of sides does not form a right triangle? 6, 8, 108, 15, 177, 24, 265, 12, 13

Step-by-step answer

P Answered by PhD

13

We know that
The triangle inequality states that for any triangle, the sum of the lengths of any two sides of a triangle is greater than the length of the third side

Part 1) Which of the following sets of possible side lengths forms a triangle?
case A) 6, 9, and 15
6+9 is not > 15

case B) 4, 10, and 15
4+10 is not > 15

case C) 10, 15, and 25
10+15 is not > 25

case D) 12, 12, and 23
12+12 is > 23> ok
12+23 is > 12> ok

the answer part 1) is
12, 12, and 23

Part 2) Which of the following sets of possible side lengths forms a right triangle?

case A) 12, 35, and 38
if the side lengths forms a right triangle
then
12²+35²=38²
12²+35²> 1369
38²> 1444

1369 is not equal to 1444

case B) 11,60, and 61
if the side lengths forms a right triangle
then
11²+60²=61²
11²+60²> 3721
61²> 3721
3721 is equal to 3721> the sides forms a right triangle

case C) 9,40 and 45
if the side lengths forms a right triangle
then
9²+40²=45²
9²+40²> 1681
45²> 2025
1681 is not 2025

case D) 6, 12, and 13
if the side lengths forms a right triangle
then
6²+12²=13²
6²+12²> 180
13²> 169
180 is not 169

the answer part 2) is
case B) 11,60, and 61 forms a right triangle

Part 3) Which of the following sets of sides does not form a right triangle?

case A) 6, 8, 10
if the side lengths forms a right triangle
then
6²+8²=10²
6²+8²> 100
10²> 100
100 is equal to 100 > the side lengths forms a right triangle

case B) 8,15,17
if the side lengths forms a right triangle
then
8²+15²=17²
8²+15²> 289
17²> 289
289 is equal to 289> the side lengths forms a right triangle

case C) 7,24,26
if the side lengths forms a right triangle
then
7²+24²=26²
7²+24²> 1176
26²> 676
1176 is not 676> the sides lengths does not form a right triangle

case D) 5,12,13
if the side lengths forms a right triangle
then
5²+12²=13²
5²+12²> 169
13²> 169
169 is equal to 169> the side lengths forms a right triangle

the answer Part 3) is
the option 7,24,26 does not form a right triangle

Mathematics

Need here : ) 5.02 1. solve the triangle. a = 50°, b = 13, c = 6 (2 points) a) a ≈ 10.2, c ≈ 26.3, b ≈ 103.7 b) a ≈ 14, c ≈ 26.3, b ≈ 103.7 c) no triangles possible d) a ≈ 14, c ≈ 30.3, b ≈ 99.7 2. solve the triangle. a = 12, b = 22, c = 95° (2 points) a) c ≈ 26, a ≈ 27.6°, b ≈ 57.4° b) c ≈ 26, a ≈ 54.4°, b ≈ 30.6° c) c ≈ 25.1, a ≈ 27.6°, b ≈ 57.4° d) c ≈ 25.1, a ≈ 31.6°, b ≈ 53.4° 3. find the area of the triangle with the given measurements. round the solution to the nearest hundredth if necessary. a = 50°, b = 30 ft, c = 14 ft (2 points) a) 160.87

Step-by-step answer

P Answered by Specialist

30

1. A.Use law of cosines. cosA=(b^2+c^2-a^2)/(2bc) because A is the included angle between b and c. Plug in A=50 degrees, b=13, c=6. cos50=(13^2+6^2-a^2)/(2*13*6), a^2=104.7,a=10.2 approximately, so choose A.

2. A.Use law of cosines again. cosC=(a^2+b^2-c^2)/(2ab). C=95 degrees, a=12, b=22. Plug in, cos95=(12^2+22^2-c^2)/(2*12*22), solve the equation, c^2=674, c=26 approximately. The use law of sines to solve for angle A (also works for B), a/sinA=c/sinC, 12/sinA=26/sin95, sinA=0.46, A=arcsin(0.46)=27.6. Choose A.

3. Answer is A. Area=1/2bc*sinA, since A is the included angle between b and c. Plug in b=30, c=14, A=50 degrees, area=1/2*14*30*sin50=160. 87, so the answer is A.

4. D. As long as the sum of any two sides of the triangle is bigger than the third, the triangle exists. 240+121>263, 240+263>121, 263+121>240, so it exists. To use Heron's formula, first find the semiperimeter, (240+263+121)/2=312. A=\sqrt(312*(312-240)*(312-263)*(312-121))=14499.7 approximately, so choose D.

5. 300. The included angle between the two paths is C=49.17+90=139.17 degrees. The lengths of the two paths are a=150, b=170. c is the distance we want. Use the law of cosines, cosC=(a^2+b^2-c^2)/(2ab). Plug in, c^2=89989, c=300 approximately.

Mathematics

The vertices of δrst are r(–1,–1), s(–1,11) and t(4,11). which could be the side lengths of a triangle that is similar but not congruent to δrst? 10, 12, and 13 units 5, 24, and 26 units 10, 24, and 26 units 5, 12, and 13 units

Step-by-step answer

P Answered by Master

29

The side lengths could be 10, 24 and 26 units.

We must first find the side lengths. We use the distance formula to do this.

For RT:
$d=\sqrt{(11--1)^2+(-1--1)^2}
\\=\sqrt{(11+1)^2+(-1+1)^2}
\\=\sqrt{12^2+0^2}=\sqrt{144}=12$

For ST:
$d=\sqrt{(11-11)^2+(4--1)^2}
\\=\sqrt{0^2+(4+1)^2}=\sqrt{5^2}=\sqrt{25}=5$

For TR:
$d=\sqrt{(11--1)^2+(4--1)^2}
\\=\sqrt{(11+1)^2+(4+1)^2}=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13$

Our side lengths, from least to greatest, are 5, 12 and 13.

To be similar but not congruent, the side lengths must have the same ratio between corresponding sides but not be the same length. 10, 24 and 26 are all 2x the original side lengths, so this works.

Mathematics

Which of the following sets of possible side lengths forms a triangle? 6, 9, and 15 4, 10, and 15 10, 15, and 25 12, 12, and 23 which of the following sets of possible side lengths forms a right triangle? 12, 35, and 3811, 60, and 619, 40, and 456, 12, and 13 which of the following sets of sides does not form a right triangle? 6, 8, 108, 15, 177, 24, 265, 12, 13

Step-by-step answer

P Answered by PhD

13

We know that
The triangle inequality states that for any triangle, the sum of the lengths of any two sides of a triangle is greater than the length of the third side

Part 1) Which of the following sets of possible side lengths forms a triangle?
case A) 6, 9, and 15
6+9 is not > 15

case B) 4, 10, and 15
4+10 is not > 15

case C) 10, 15, and 25
10+15 is not > 25

case D) 12, 12, and 23
12+12 is > 23> ok
12+23 is > 12> ok

the answer part 1) is
12, 12, and 23

Part 2) Which of the following sets of possible side lengths forms a right triangle?

case A) 12, 35, and 38
if the side lengths forms a right triangle
then
12²+35²=38²
12²+35²> 1369
38²> 1444

1369 is not equal to 1444

case B) 11,60, and 61
if the side lengths forms a right triangle
then
11²+60²=61²
11²+60²> 3721
61²> 3721
3721 is equal to 3721> the sides forms a right triangle

case C) 9,40 and 45
if the side lengths forms a right triangle
then
9²+40²=45²
9²+40²> 1681
45²> 2025
1681 is not 2025

case D) 6, 12, and 13
if the side lengths forms a right triangle
then
6²+12²=13²
6²+12²> 180
13²> 169
180 is not 169

the answer part 2) is
case B) 11,60, and 61 forms a right triangle

Part 3) Which of the following sets of sides does not form a right triangle?

case A) 6, 8, 10
if the side lengths forms a right triangle
then
6²+8²=10²
6²+8²> 100
10²> 100
100 is equal to 100 > the side lengths forms a right triangle

case B) 8,15,17
if the side lengths forms a right triangle
then
8²+15²=17²
8²+15²> 289
17²> 289
289 is equal to 289> the side lengths forms a right triangle

case C) 7,24,26
if the side lengths forms a right triangle
then
7²+24²=26²
7²+24²> 1176
26²> 676
1176 is not 676> the sides lengths does not form a right triangle

case D) 5,12,13
if the side lengths forms a right triangle
then
5²+12²=13²
5²+12²> 169
13²> 169
169 is equal to 169> the side lengths forms a right triangle

the answer Part 3) is
the option 7,24,26 does not form a right triangle

The side lengths of a triangle are 10,26 and 24 which one is the hypotenuse a.24
b.26
c.10
d.50

Step-by-step answer

Faq

Try asking the Studen AI a question.

The side lengths of a triangle are 10,26 and 24 which one is the hypotenuse a.24b.26c.10d.50

Step-by-step answer

Faq

Try asking the Studen AI a question.

The side lengths of a triangle are 10,26 and 24 which one is the hypotenuse a.24
b.26
c.10
d.50