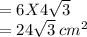What is the formula of equilateral triangle .class-8, №18011049, 03.11.2022 15:01

Mathematics

What is the formula of equilateral triangle .class-8

Step-by-step answer

P Answered by Master

Step-by-step explanation:

The perimeter of an equilateral triangle is:

P = 3a (where a any length of the triangle)

The area of an equilateral triangle is:

$A = \frac{\sqrt{3} }{4} a^{2}$ (where a is the side length)

Using the area formula we can rearrange it to get the formula of the length of the equilateral triangle:

$a = \frac{2}{3} 3^{\frac{3}{4} } \sqrt{A}$

Mathematics

Comparing Familiar Area Formulas Bianca calculated the height of the equilateral triangle with side lengths of 10 Calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare it to Bianca s answer. The apothem, rounded to the nearest tenth, is units. The perimeter of the equilateral triangle is units. Therefore, the area of the equilateral triangle is vor approximately 43.5 units The calculated areas are tan(30) = n = 8.7 rebo Then, she used the formula for area of a triangle to approximate its area,

Step-by-step answer

P Answered by Master

89

1. 2.9 units

2. 30 units

3. 1/2(2.9)(30)

4. the same despite using different formulas

Step-by-step explanation:

Mathematics

Comparing Familiar Area Formulas Bianca calculated the height of the equilateral triangle with side lengths of 10 Calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare it to Bianca s answer. The apothem, rounded to the nearest tenth, is units. The perimeter of the equilateral triangle is units. Therefore, the area of the equilateral triangle is vor approximately 43.5 units The calculated areas are tan(30) = n = 8.7 rebo Then, she used the formula for area of a triangle to approximate its area,

Step-by-step answer

P Answered by Master

89

1. 2.9 units

2. 30 units

3. 1/2(2.9)(30)

4. the same despite using different formulas

Step-by-step explanation:

Mathematics

Bianca calculated the height of the equilateral triangle with side lengths of 10. tangent (30) = StartFraction 5 Over h EndFraction An equilateral triangle with side lengths of 10 is shown. A bisector is drawn to split the side into 2 equal parts and splits the angle into 2 30 degree segments. Then, she used the formula for area of a triangle to approximate its area, as shown below. A = one-half b h. = one-half (10) (8.7). = 43.5 units squared. Calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare

Step-by-step answer

P Answered by PhD

6

43.5 units squared

Step-by-step explanation:

The area of a regular polygon is given as:

$= \frac{1}{2} ap$

'a' is the apothem and 'p' is the perimeter.

The perimeter of the equilateral triangle is 3×10=30 units.

The apothem is given by:

$a = \frac{s}{2 \sqrt{3} }$

$a = \frac{10}{2 \sqrt{3} }$

a = 2.9

Therefore the area is

$\frac{1}{2} \times 2.9 \times 30 = 43.5$

Mathematics

Bianca calculated the height of the equilateral triangle with side lengths of 10. tangent (30) = StartFraction 5 Over h EndFraction An equilateral triangle with side lengths of 10 is shown. A bisector is drawn to split the side into 2 equal parts and splits the angle into 2 30 degree segments. Then, she used the formula for area of a triangle to approximate its area, as shown below. A = one-half b h. = one-half (10) (8.7). = 43.5 units squared. Calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare

Step-by-step answer

P Answered by PhD

6

43.5 units squared

Step-by-step explanation:

The area of a regular polygon is given as:

$= \frac{1}{2} ap$

'a' is the apothem and 'p' is the perimeter.

The perimeter of the equilateral triangle is 3×10=30 units.

The apothem is given by:

$a = \frac{s}{2 \sqrt{3} }$

$a = \frac{10}{2 \sqrt{3} }$

a = 2.9

Therefore the area is

$\frac{1}{2} \times 2.9 \times 30 = 43.5$

Mathematics

Bianca calculated the height of the equilateral triangle with side lengths of 10. then, she used the formula for area of a triangle to approximate its area, as shown below. calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare it to bianca’s answer. the apothem, rounded to the nearest tenth, is . the perimeter of the equilateral triangle is . therefore, the area of the equilateral triangle , or approximately 43.5 units2. the calculated areas

Step-by-step answer

P Answered by PhD

1) - A. 2.3

2) - C. 30

3) - A. 1/2(2.9)(30)

4) - D. The same, despite using different formulas.

Just took quiz.

Mathematics

Bianca calculated the height of the equilateral triangle with side lengths of 10. then, she used the formula for area of a triangle to approximate its area, as shown below. calculate the area of the equilateral triangle using the formula for area of a regular polygon, and compare it to bianca’s answer. the apothem, rounded to the nearest tenth, is . the perimeter of the equilateral triangle is . therefore, the area of the equilateral triangle , or approximately 43.5 units2. the calculated areas

Step-by-step answer

P Answered by PhD

1) - A. 2.3

2) - C. 30

3) - A. 1/2(2.9)(30)

4) - D. The same, despite using different formulas.

Just took quiz.

Mathematics

Score for Question 3: ___ of 5 points) 3. Use the diagram of a REGULAR HEXAGON and follow these steps to solve for the area of a hexagon with sides equal to 4 cm. Leave radicals in your answers. How many equilateral triangles are there? If we cut an equilateral down the middle (green line) what special triangle do you create? Sketch and label all side lengths of the 30-60-90 triangle by itself below. What is the length of the short side of one 30-60-90 triangle? What is the length of the hypotenuse of one 30-60-90 triangle? Apply properties of

Step-by-step answer

P Answered by PhD

3

(a)6 Equilateral Triangles.

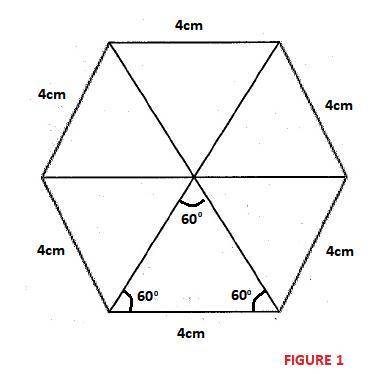
(b)30-60-90 triangle.

(c)See Attached Triangle in Figure 2

(d)Length of the short leg = 2cm.

(e)Length of the hypotenuse= 4cm.

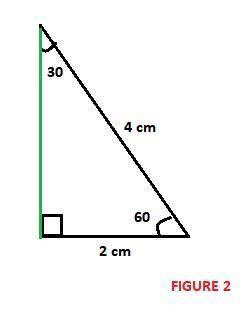
(f)Length of the long leg=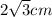 $2\sqrt{3}cm$

(g)Apothem.

(h)Height of the Equilateral triangle=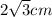 $2\sqrt{3}cm$

(i)Area of One Equilateral triangle =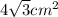 $4\sqrt{3}cm^2$

(j)Area of Hexagon =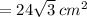 $=24\sqrt{3}\:cm^2$

Step-by-step explanation:

(a)From Figure 1, there are 6 Equilateral Triangles.

(b)If we cut an equilateral down the middle (green line), we create a 30-60-90 triangle.

(c)Triangle Attached in Figure 2.

(d)The length of the short leg of one of the 30-60-90 triangle is 2cm.

(e)The length of the hypotenuse of one of the 30-60-90 triangle is 4cm.

(f)Length of the long leg

We use Pythagoras Theorem to find the length of the long leg of the right triangle.

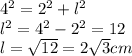
$4^2=2^2+l^2\\l^2=4^2-2^2=12\\l=\sqrt{12}=2\sqrt{3}cm$

(g)The vocabulary word for the long side of the 30-60-90 called in the polygon (green line) is Apothem.

It is line segment from the center to the midpoint of one of the sides of a polygon.

(h)Height of the Equilateral Triangle=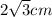 $2\sqrt{3}cm$

(i)Area of One Equilateral triangle

Base =4 cm, Height =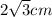 $2\sqrt{3}cm$

Area=0.5X4X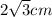 $2\sqrt{3}cm$

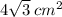
= $4\sqrt{3}\:cm^2$

(j)Area of Hexagon =Area of One Equilateral Triangle X 6

$=6X 4\sqrt{3}\\=24\sqrt{3}\:cm^2$

Score for Question 3: ___ of 5 points) 3. Use the diagram of a REGULAR HEXAGON and follow these step

Mathematics

(Score for Question 3 of 5 points) 3. Use the diagram of a REGULAR HEXAGON and follow these steps to solve for the area of a hexagon with sides equal to 4 cm. Leave radicals in your answers, How many equilateral triangles are there?. If we cut an equilateral down the middle (green line) what special triangle do you create? Sketch and label all side lengths of the 30-60-90 triangle by itself below. What is the length of the short side of one 30-60-90 triangle? _ What is the length of the hypotenuse of one 30-60-90 triangle? Apply properties of 30-60-90

Step-by-step answer

P Answered by PhD

4

Regular Hexagon area H = 24 $\sqrt{3}$ sq. cm.

In a regular Hexagon, there are 6 equilateral triangles.

You create a 30-60-90 triangle when you cut an equilateral triangle in half.

The long side of the 30-60-90 triangle is called the "apothem"

Step-by-step explanation:

You have one side of 4cm for the regular hexagon.

so then the shortest side of the 30-60-90 triangle is 2 cm.

the hypotenuse is therefore 4cm

and the long leg is equal to 2*root(3)

Height of one equilateral triangle = 2 root(3) cm.

Area of one of these equilateral triangles : A = (1/2)*2*root(3)*4cm

A = 4 root(3) sq. cm is area of one equilateral triangle.

Hexagon area : H = 6*A = 6*4*root(3) = 24 root(3)

H = 24 $\sqrt{3}$ sq. cm.

Mathematics

1. the prism-shaped roof has equilateral triangular bases. create an equation that models the height of one of the roof s triangular bases in terms of its sides. in your final answer, include all necessary calculations. 2. the prism-shaped roof has equilateral triangular bases. use the model you created in question #1 to calculate the height of the roof, to the nearest tenth of a foot, if the side lengths each measure 25 feet. in your final answer, include all necessary calculations. 3. to determine the amount of roofing materials needed, the area

Step-by-step answer

P Answered by PhD

38

1. Check picture 1. Let the one side of the triangle be a, drop one perpendicular, CD. Then triangle ADB is a right triangle, with hypothenuse a and one side equal to 1/2a. By the Pythegorean theorem, as shown in the picture, the height is $\frac{ \sqrt{3} }{2} a$

2. if a a=25 ft, then the height is $\frac{ \sqrt{3} }{2} a=\frac{ \sqrt{3} }{2} *25= \frac{1.732}{2}*25= 21. 7$ (ft)

3. consider picture 2. Let the length of the roof be l feet.

one side of the prism (the roof) is a rectangle with dimensions a and l, so the area of one side is a*l
the lateral Area of the roof is 3a*l

the area of the equilateral surfaces is $2*( \frac{1}{2} *a* \frac{ \sqrt{3} }{2}a )=\frac{ \sqrt{3} }{2} a^{2}$

so the total area of the roof is $\frac{ \sqrt{3} }{2} a^{2} +3al$

4. The total area was the 2 triangular surfaces + the 3 equal lateral rectangular surfaces. Now instead of 3 lateral triangular surfaces, we have 2.
So the total area found previously will be decreased by al

5. so the area now is $\frac{ \sqrt{3} }{2} a^{2} +2al$

6. now a=25 and l=2a=50

Area= $\frac{ \sqrt{3} }{2} a^{2} +2al=\frac{ \sqrt{3} }{2} * 25^{2}+2*25*50=25 ^{2} (\frac{ \sqrt{3} }{2} +4)=625*4.866$

=3041.3 (ft squared)

1. the prism-shaped roof has equilateral triangular bases. create an equation that models the height

1. the prism-shaped roof has equilateral triangular bases. create an equation that models the height

What is the formula of equilateral triangle .class-8

Step-by-step answer

Faq

Try asking the Studen AI a question.