Which of the following best represents the graph of the line of the equation x + 5y = 15?

Letter C

Step-by-step explanation:

Slope: -

Y-intercept: 3

y = - + 3

y=12x+5 answer choice B, 89 kilometers

Step-by-step explanation:

y=12x+5 answer choice B, 89 kilometers

Step-by-step explanation:

Infinitely many solutions.

They must satisfy

Step-by-step explanation:

Given

Required

The best description

Add both equations

---- this means that the system has infinitely many solutions.

Make y the subject in:

Add x to both sides

Divide through by 5

Hence, they must satisfy:

Infinitely many solutions.

They must satisfy

Step-by-step explanation:

Given

Required

The best description

Add both equations

---- this means that the system has infinitely many solutions.

Make y the subject in:

Add x to both sides

Divide through by 5

Hence, they must satisfy:

19 substitution

20 elimination

21 elimination

22 elimination

Step-by-step explanation:

19.) x + y = 2

y = 2x - 1

Substitution, since the second equation is already solved for y

x + (2x-1) =2

Combine like terms

3x-1 =2

Add 1 to each side

3x-1+1= 2+1

3x=3

Divide by 3

x=1

Now we need y

x+y =2

1+y= 2

Subtract 1

y=1

(1,1)

20.) - x - 5y = 7

x + y = 1

I will used elimination since  there is an x and a -x

- x - 5y = 7

x + y = 1

-4y = 8

Divide by -4

-4y/-4 = 8/-4

y = -2

x+y =1

x-2=1

Add 2 to each side

x-2+2=1+2

x=3

(3,-2)

21.) 3x + y = 26

3x + 3y = 26

I will use elimination by multiplying the second equation by -1

3x + y = 26

-3x - 3y = -26

   -2y = 0

Divide by -2

-2y/-2 = 0/-2

y =0

Now we need to find x

3x + 0 = 26

Divid by 3

3x/3  = 26/3

x = 26/3

(26/3 ,0)

22.) 4x - 8y = 52

7x + 4y = 1

I will use elimination by multiplying the second equation by 2

2( 7x + 4y = 1 )

14x +8y =2

The add this to the first equation to eliminate y

4x - 8y = 52

14x +8y =2

18x = 54

Divide by 18

18x/18 = 54/18

x=3

Now we need to find y

7x + 4y = 1

7(3) +4y = 1

21 +4y = 1

Subtract 21 from each side

21-21 +4y = 1-21

4y = -20

Divide by 4

4y/4 = -20/4

y=-5

(3,-5)

19 substitution

20 elimination

21 elimination

22 elimination

Step-by-step explanation:

19.) x + y = 2

y = 2x - 1

Substitution, since the second equation is already solved for y

x + (2x-1) =2

Combine like terms

3x-1 =2

Add 1 to each side

3x-1+1= 2+1

3x=3

Divide by 3

x=1

Now we need y

x+y =2

1+y= 2

Subtract 1

y=1

(1,1)

20.) - x - 5y = 7

x + y = 1

I will used elimination since  there is an x and a -x

- x - 5y = 7

x + y = 1

-4y = 8

Divide by -4

-4y/-4 = 8/-4

y = -2

x+y =1

x-2=1

Add 2 to each side

x-2+2=1+2

x=3

(3,-2)

21.) 3x + y = 26

3x + 3y = 26

I will use elimination by multiplying the second equation by -1

3x + y = 26

-3x - 3y = -26

   -2y = 0

Divide by -2

-2y/-2 = 0/-2

y =0

Now we need to find x

3x + 0 = 26

Divid by 3

3x/3  = 26/3

x = 26/3

(26/3 ,0)

22.) 4x - 8y = 52

7x + 4y = 1

I will use elimination by multiplying the second equation by 2

2( 7x + 4y = 1 )

14x +8y =2

The add this to the first equation to eliminate y

4x - 8y = 52

14x +8y =2

18x = 54

Divide by 18

18x/18 = 54/18

x=3

Now we need to find y

7x + 4y = 1

7(3) +4y = 1

21 +4y = 1

Subtract 21 from each side

21-21 +4y = 1-21

4y = -20

Divide by 4

4y/4 = -20/4

y=-5

(3,-5)

OPTION A

Step-by-step explanation:

The equation of the line in slope-intercept form is:

Where m is the slope and b the y-intercept.

Solve for y from each equation:

As you can see the slope and the y-intercept of each equation are equal, this means that both are the exact same line. Therefore, you can conclude that the system has infinitely many solutions.

Yes, Lisa will get the same solution no matter what method she applies. The reason is that we have been given 2 equations. As these are linear equations, both of the equations represent 2 different lines having different slopes. The solution of two different lines is taken as the point of intersection of both lines, because that is the only point that lies on both lines. This point will always remain the same for two particular lines. So whatever method Lisa applies, the point of intersection will always remain the same i.e (5,1)

Yes, the answer to A will change if the systems of equation has no solution. If system of equations have no solution, it means the both lines never intersect, which happens for parallel line. Hence, there is no point of intersection.

Yes, the answer to A will change if the systems of equation has infinite many solution. It means that both lines intersect at every point of each line, which happens when both lines overlap each other. Hence, the point of intersection, which represents the solution, is every point of both lines.

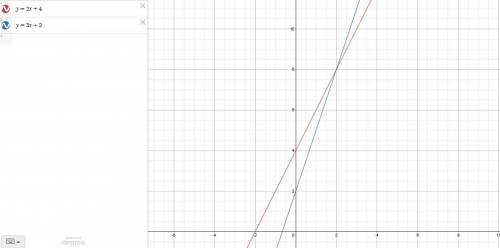
The graph of both equations is given below.

The solution is the point of intersection of both line

As both lines intersect a x = 2 and y = 8.

Solution: (2,8)

OPTION A

Step-by-step explanation:

The equation of the line in slope-intercept form is:

Where m is the slope and b the y-intercept.

Solve for y from each equation:

As you can see the slope and the y-intercept of each equation are equal, this means that both are the exact same line. Therefore, you can conclude that the system has infinitely many solutions.