Whats the constant propionality, №18011190, 06.05.2021 13:45

Mathematics

Step-by-step answer

P Answered by Specialist

3/2

Explanation:

find where the line hits perfectly on a corner and divide the x by the y, in this case one of the options is 6 divided 4 which is 1.5 (3/2)

Whats the constant propionality

Chemistry

When comparing propionic acid (ch3ch2cooh) and sodium propionate (ch3ch2coona), the one that is more soluble in water is when comparing propionic acid ( c h 3 c h 2 c o o h ) and sodium propionate ( c h 3 c h 2 c o o n a ), the one that is more soluble in water is blank.. when comparing cyclohexane (c6h12) and glucose (c6h12o6), the one that is more soluble in water is when comparing cyclohexane ( c 6 h 12 ) and glucose ( c 6 h 12 o 6 ), the one that is more soluble in water is blank.. when comparing hydrochloric acid (hcl) and ethyl chloride (ch3ch2cl),

Step-by-step answer

P Answered by Master

2

When comparing propionic acid (CH₃CH₂COOH) and sodium propionate (CH₃CH₂COONa), the one that is more soluble in water sodium propionate.

When comparing cyclohexane (C6H12) and glucose (C6H12O6), the one that is more soluble in water is glucose

When comparing hydrochloric acid (HCl) and ethyl chloride (CH3CH2Cl), the one that is more soluble in water is hydrochloric acid

Explanation:

When comparing propionic acid (CH₃CH₂COOH) and sodium propionate (CH₃CH₂COONa), the one that is more soluble in water sodium propionate. Because always a salt is more soluble in water than its acid (Solubility of propionic acid is 0,37g/mL and of sodium propionate is 1g/mL).

When comparing cyclohexane (C6H12) and glucose (C6H12O6), the one that is more soluble in water is glucose because cyclohexane is made from petroleum and its polarity is very low (cyclohexane is insoluble in water and solubility of glucose is 0,91g/mL).

When comparing hydrochloric acid (HCl) and ethyl chloride (CH3CH2Cl), the one that is more soluble in water is hydrochloric acid because an acid has a medium-high solubility in water but, again, an alkane derived from petroleum has very low solubility in water (hydrochloric acid has a solubility of 0,823g/mL and ethyl chloride is insoluble in water).

I hope it helps!

Chemistry

When comparing propionic acid (ch3ch2cooh) and sodium propionate (ch3ch2coona), the one that is more soluble in water is when comparing propionic acid ( c h 3 c h 2 c o o h ) and sodium propionate ( c h 3 c h 2 c o o n a ), the one that is more soluble in water is blank.. when comparing cyclohexane (c6h12) and glucose (c6h12o6), the one that is more soluble in water is when comparing cyclohexane ( c 6 h 12 ) and glucose ( c 6 h 12 o 6 ), the one that is more soluble in water is blank.. when comparing hydrochloric acid (hcl) and ethyl chloride (ch3ch2cl),

Step-by-step answer

P Answered by Specialist

2

When comparing propionic acid (CH₃CH₂COOH) and sodium propionate (CH₃CH₂COONa), the one that is more soluble in water sodium propionate.

When comparing cyclohexane (C6H12) and glucose (C6H12O6), the one that is more soluble in water is glucose

When comparing hydrochloric acid (HCl) and ethyl chloride (CH3CH2Cl), the one that is more soluble in water is hydrochloric acid

Explanation:

When comparing propionic acid (CH₃CH₂COOH) and sodium propionate (CH₃CH₂COONa), the one that is more soluble in water sodium propionate. Because always a salt is more soluble in water than its acid (Solubility of propionic acid is 0,37g/mL and of sodium propionate is 1g/mL).

When comparing cyclohexane (C6H12) and glucose (C6H12O6), the one that is more soluble in water is glucose because cyclohexane is made from petroleum and its polarity is very low (cyclohexane is insoluble in water and solubility of glucose is 0,91g/mL).

When comparing hydrochloric acid (HCl) and ethyl chloride (CH3CH2Cl), the one that is more soluble in water is hydrochloric acid because an acid has a medium-high solubility in water but, again, an alkane derived from petroleum has very low solubility in water (hydrochloric acid has a solubility of 0,823g/mL and ethyl chloride is insoluble in water).

I hope it helps!

Chemistry

The acid dissociation ka of propionic acid c2h5co2h is 1.310x10−5. calculate the ph of a 3.010x10−4m aqueous solution of propionic acid. round your answer to 2 decimal places.

Step-by-step answer

P Answered by Specialist

Answer : The pH of the solution is, 4.25

Solution : Given,

Concentration (C) = $3.010\times 10^{-4}M$

Acid dissociation constant = $k_a=1.310\times 10^{-5}$

The equilibrium reaction for dissociation of C_2H_5CO_2H (weak acid) is,

$C_2H_5CO_2H\rightleftharpoons C_2H_5CO_2^-+H^+$

initially conc. c 0 0

At eqm. $c(1-\alpha)$ $c\alpha$ $c\alpha$

where, $\alpha$ is degree of dissociation

First we have to calculate the value of $\alpha$

$K_a=\frac{(c\alpha)\times (c\alpha)}{c(1-\alpha)}$

$K_a=\frac{c(\alpha)^2}{(1-\alpha)}$

Now put all the given values in this formula, we get:

$1.310\times 10^{-5}=\frac{(3.010\times 10^{-4})(\alpha)^2}{(1-\alpha)}$

$\alpha=0.188$

Now we have to calculate the hydrogen ion concentration.

$[H^+]=c\alpha=(3.010\times 10^{-4})\times (0.188)=5.66\times 10^{-5}M$

Now we have to calculate the pH.

$pH=-\log [H^+]$

$pH=-\log (5.66\times 10^{-5})$

pH=4.25

Therefore, the pH of the solution is, 4.25

Chemistry

A buffer contains 0.17 mol of propionic acid ( C2H5COOH ) and 0.14 mol of sodium propionate (C2H5COONa) in 1.20 L.What is the pH of the buffer after the addition of 0.01 mol of HI

Step-by-step answer

P Answered by Specialist

The pH of the buffer after addition of given amount of HI is 4.76

Explanation:

We are given:

Initial moles of propionic acid = 0.17 moles

Initial moles of sodium propionate = 0.14 moles

Moles of HI added = 0.01 moles

The chemical equation for the reaction of HI and sodium propionate follows:

$C_2H_5COONa+HI\rightleftharpoons C_2H_5COOH+NaI$

Initial: 0.14 0.01 0.17

At eqllm: 0.13 - 0.18

Total volume of the container = 1.20 L

To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

$pH=pK_a+\log(\frac{[salt]}{[acid]})$

$pH=pK_a+\log(\frac{[C_2H_5COONa]}{[C_2H_5COOH]})$

We are given:

pK_a = negative logarithm of acid dissociation constant of propionic acid = 4.87

$[C_2H_5COONa]=\frac{0.14}{1.20}$

$[C_2H_5COOH]=\frac{0.18}{1.20}$

pH = ?

Putting values in above equation, we get:

$pH=4.87+\log(\frac{0.14/1.20}{0.18/1.20})\\\\pH=4.76$

Hence, the pH of the buffer after addition of given amount of HI is 4.76

Chemistry

An analytical chemist is titrating of a solution of propionic acid with a solution of 224.9 ml of a 0.6100M solution of propionic acid (HC2H5CO2) with a 1.1000M solution of KOH. The pKa of proionic acid 4.89. Calculate the pH of the acid solution after the chemist has added 41.04mL of the KOH solution to it. Note for advanced students: you may assume the final volume equals the initial volume of the solution plus the volume of solution added. Round your answer to decimal places.

Step-by-step answer

P Answered by Specialist

1

The pH of acid solution is 4.58

Explanation:

To calculate the number of moles for given molarity, we use the equation:

$\text{Molarity of the solution}=\frac{\text{Moles of solute}\times 1000}{\text{Volume of solution (in mL)}}$ .....(1)

For KOH:

Molarity of KOH solution = 1.1000 M

Volume of solution = 41.04 mL

Putting values in equation 1, we get:

$1.1000M=\frac{\text{Moles of KOH}\times 1000}{41.04}\\\\\text{Moles of KOH}=\frac{1.1000\times 41.04}{1000}=0.04514mol$

For propanoic acid:

Molarity of propanoic acid solution = 0.6100 M

Volume of solution = 224.9 mL

Putting values in equation 1, we get:

$0.6100M=\frac{\text{Moles of propanoic acid}\times 1000}{224.9}\\\\\text{Moles of propanoic acid}=\frac{0.6100\times 224.9}{1000}=0.1372mol$

The chemical reaction for propanoic acid and KOH follows the equation:

$C_2H_5COOH+KOH\rightarrow C_2H_5COOK+H_2O$

Initial: 0.1372 0.04514

Final: 0.09206 - 0.04514

Total volume of solution = [224.9 + 41.04] mL = 265.94 mL = 0.26594 L (Conversion factor: 1 L = 1000 mL)

To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

$pH=pK_a+\log(\frac{[\text{salt}]}{[acid]})$

$pH=pK_a+\log(\frac{[C_2H_5COOK]}{[C_2H_5COOH]})$

We are given:

pK_a = negative logarithm of acid dissociation constant of propanoic acid = 4.89

$[C_2H_5COOK]=\frac{0.04514}{0.26594}$

$[C_2H_5COOH]=\frac{0.09206}{0.26594}$

pH = ?

Putting values in above equation, we get:

$pH=4.89+\log(\frac{(0.04514/0.26594)}{(0.09206/0.26594)})\\\\pH=4.58$

Hence, the pH of acid solution is 4.58

Chemistry

For the gas phase decomposition of t-butyl propionate,C2H5COOC(CH3)3 (CH3)2C=CH2 + C2H5COOHthe rate constant at 540 K is 8.90×10-4 s-1 and the rate constant at 578 K is 9.83×10-3 s-1. The activation energy for the gas phase decomposition of t-butyl propionate is kJ/mol.

Step-by-step answer

P Answered by Specialist

The activation energy is 164.02 kJ/mol

Explanation:

Log (k2/k1) = Ea/2.303R × [1/T1 - 1/T2]

k1 = 8.9×10^-4 s^-1

k2 = 9.83×10^-3 s^-1

R = 8.314 J/mol.K

T1 = 540 K

T2 = 578 K

Log (9.83×10^-3/8.9×10^-4) = Ea/2.303×8.314 × [1/540 - 1/578]

1.043 = 6.359×10^-6Ea

Ea = 1.043/6.359×10^-6 = 164020 J/mol = 164020/1000 = 164.02 kJ/mol

Chemistry

Asolution prepared by dissolving 0.100 mole of propionic acid in enough water to make 1.00 l of solution is observed to have a ph = 2.94. what is the ka for propionic acid? (a) 1.3 x 10¯6(b) 1.1 x 10¯3(c) 1.3 x 10¯5(d) 1.1 x 10¯2

Step-by-step answer

P Answered by PhD

C) $k_a=1.3\times 10^{-5}$

Explanation:

pH is defined as the negative logarithm of the concentration of hydrogen ions.

Thus,

pH = - log [H⁺]

The expression of the pH of the calculation of weak acid is:-

$pH=-log(\sqrt{k_a\times C})$

Where, C is the concentration = 0.5 M

Given, pH = 2.94

Moles = 0.100 moles

Volume = 1.00 L

So, $Molarity=\frac{Moles}{Volume}=\frac{0.100}{1.00}\ M=0.100\ M$

C = 0.100 M

$2.94=-log(\sqrt{k_a\times 0.100})$

$\log _{10}\left(\sqrt{k_a0.1}\right)=-2.94$

$\sqrt{0.1}\sqrt{k_a}=\frac{1}{10^{2.94}}$

$k_a=1.3\times 10^{-5}$

Chemistry

Abuffer contains 0.19 mol of propionic acid (c2h5cooh) and 0.26 mol of sodium propionate (c2h5coona) in 1.20 l. you may want to reference (pages 721 - 729) section 17.2 while completing this problem. part a what is the ph of this buffer? express the ph to two decimal places. php h = nothing request answer part b what is the ph of the buffer after the addition of 0.02 mol of naoh? express the ph to two decimal places. php h = nothing request answer part c what is the ph of the buffer after the addition of 0.02 mol of hi? express the ph to two decimal

Step-by-step answer

P Answered by Master

Explanation:

It is known that 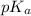$pK_{a}$ of propionic acid = 4.87

And, initial concentration of propionic acid = 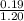$\frac{0.19}{1.20}$

= 0.158 M

Concentration of sodium propionate = \frac{0.26}{1.20}[/tex]

= 0.216 M

Now, in the given situation only propionic acid and sodium propionate are present .

Hence, pH = $pK_{a} + log(\frac{[salt]}{[acid]})$

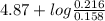
= $4.87 + log \frac{0.216}{0.158}$

= 4.87 + log (1.36)

= 5.00

Therefore, when 0.02 mol NaOH is added then,

Moles of propionic acid = 0.19 - 0.02

= 0.17 mol

Hence, concentration of propionic acid = 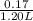$\frac{0.17}{1.20 L}$

= 0.14 M

and, moles of sodium propionic acid = (0.26 + 0.02) mol

= 0.28 mol

Hence, concentration of sodium propionic acid will be calculated as follows.

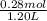
$\frac{0.28 mol}{1.20 L}$

= 0.23 M

Therefore, calculate the pH upon addition of 0.02 mol of NaOH as follows.

pH = $pK_{a} + log(\frac{[salt]}{[acid]})$

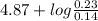
= $4.87 + log \frac{0.23}{0.14}$

= 4.87 + log (1.64)

= 5.08

Hence, the pH of the buffer after the addition of 0.02 mol of NaOH is 5.08.

Therefore, when 0.02 mol HI is added then,

Moles of propionic acid = 0.19 + 0.02

= 0.21 mol

Hence, concentration of propionic acid = 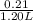$\frac{0.21}{1.20 L}$

= 0.175 M

and, moles of sodium propionic acid = (0.26 - 0.02) mol

= 0.24 mol

Hence, concentration of sodium propionic acid will be calculated as follows.

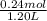
$\frac{0.24 mol}{1.20 L}$

= 0.2 M

Therefore, calculate pH upon addition of 0.02 mol of HI as follows.

pH = $pK_{a} + log(\frac{[salt]}{[acid]})$

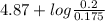
= $4.87 + log \frac{0.2}{0.175}$

= 4.87 + log (0.114)

= 4.98

Hence, the pH of the buffer after the addition of 0.02 mol of HI is 4.98.

Chemistry

A25.00-ml sample of propionic acid, hc3h5o2, of unknown concentration was titrated with 0.141 m koh. the equivalence point was reached when 43.76 ml of base had been added. what is the hydroxide-ion concentration at the equivalence point? ka for propionic acid is 1.3 × 10–5 at 25°c. a. 1.5 × 10-9 m b. 1.1 × 10-3 m c. 1.1 × 10-5 m d. 8.3 × 10-6 m e. 1.0 × 10-7 m

Step-by-step answer

P Answered by Specialist

Concentration of hydroxide-ion at equivalence point = $8.3\times 10^{-6}M$

Explanation:

$HC_{3}H_{5}O_{2}+KOH\rightarrow C_{3}H_{5}O_{2}^{-}K^{+}+H_{2}O$

1 mol of $HC_{3}H_{5}O_{2}$ reacts with 1 mol of KOH to produce 1 mol of $C_{3}H_{5}O_{2}^{-}$

At equivalence point, all $HC_{3}H_{5}O_{2}$ gets converted to $C_{3}H_{5}O_{2}^{-}$ .

Moles of $C_{3}H_{5}O_{2}^{-}$ produced at equivalence point is equal to moles of KOH added to reach equivalence point.

So, moles of $C_{3}H_{5}O_{2}^{-}$ produced = $\frac{43.76\times 0.141}{1000}moles=0.00617moles$

Total volume of solution at equivalence point = (25.00+43.76) mL = 68.76 mL

Concentration of $C_{3}H_{5}O_{2}^{-}$ at equivalence point = $\frac{0.00617\times 1000}{68.76}M=0.0897M$

$OH^{-}$ produced at equivalence point is due to hydrolysis of $C_{3}H_{5}O_{2}^{-}$ . We have to construct an ICE table to calculate concentration of $OH^{-}$ at equivalence point.