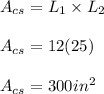FIRST.
64 square inches matches to a cross section parallel to the base of a right rectangle prism that is 3 inches long, 7 inches wide, and 11 inches tall
This is shown in the first figure below. A right rectangular prism where every edge connecting its base and the opposite face makes right angles with both faces. Since the tall is the side that measures 11 inches, then the base is formed by 3 inches long and 7 inches wide. Therefore, the area of this shape can be found as the area of a rectangle, which is:
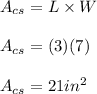
SECOND.
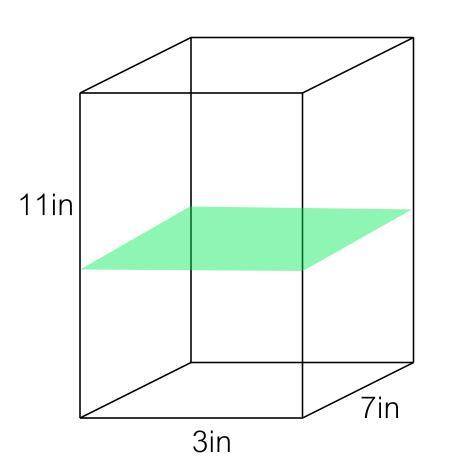
64 square inches matches to a cross section parallel to the base of a cube whose edges are 8 inches long.
This is shown in the second figure below. A cube is a prism whose sides all have the same length and in this case is 8 inches. We name cross section is to the slice that cuts through a solid. If the cross section is parallel to the base of a cube, then it forms a square with length 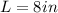 . Therefore, the area of this shape can be found as the area of a square, which is:
. Therefore, the area of this shape can be found as the area of a square, which is:
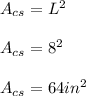
Third.
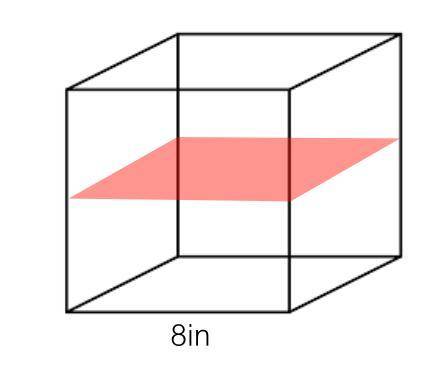
7 square inches matches to a cross section passing through the diagonal of opposite faces of a cube with edges that are 7 inches long and a diagonal that is approximately 10 inches
This is shown in the third figure below. As you can see, the cross section passes through the diagonals of the base and the top of the cube that are two opposite faces. This form a rectangle having sides 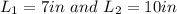 where:
where:
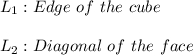
So:
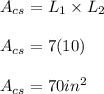
FOURTH.
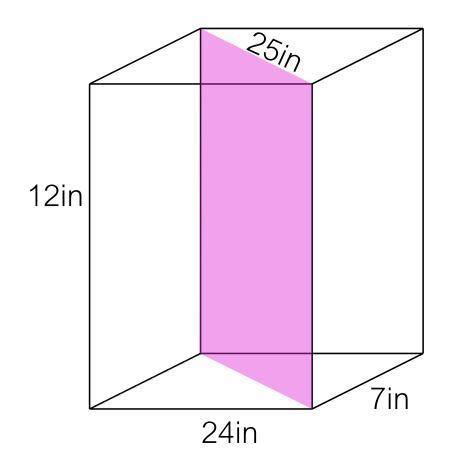
300 square inches matches to a cross section perpendicular to the base and passing through the diagonals of the base and opposite face of a right rectangular prism that is 24 inches wide, 7 inches long, and 12 inches tall and measures 25 inches along the diagonal of the base.
This is shown in the fourth figure below. The cross section passes through the diagonals of the base and the top of the right rectangular prism. They are opposite to each other, so the shape of the cross section is a rectangle whose sides are 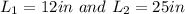 where:
where:
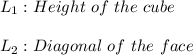
So: