Mathematics: Which expression can be used to find AC

(Sin a)/a=(sin b)/b=(sin c)/c Sry my handwriting is not great...

Which expression can be used to find AC, №18011196, 06.05.2021 13:45

Computers and Technology

In this challenge you will use the file regex_replace_challenge_student.py to: Write a regular expression that will replace all occurrences of: regular-expression regular:expression regular&expression In the string: This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression Assign the regular expression to a variable named pattern Using the sub() method from the re package substitute all occurrences of the pattern with substitution Assign the outcome of the

Step-by-step answer

P Answered by PhD

Please follow the code indentation for the python program.

Explanation:

Computers and Technology

In this challenge you will use the file regex_replace_challenge_student.py to: Write a regular expression that will replace all occurrences of: regular-expression regular:expression regular&expression In the string: This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression Assign the regular expression to a variable named pattern Using the sub() method from the re package substitute all occurrences of the pattern with substitution Assign the outcome of the

Step-by-step answer

P Answered by PhD

Please follow the code indentation for the python program.

Explanation:

Mathematics

John claims the following two expressions are equivalent. - 215y - 3) = - 10y - 6 John s work in determining an expression equivalent to the first expression is shown below. - 2/5y - 3) = (-2x5y) - (-2x - 3) = - 10y-6 Which statement explains why John s claim is incorrect? He should have subtracted (-2 * 3) resulting in the expression–10y + 6. He should have only multiplied 3 by -2 resulting in the expression 5y - 6. He should have only multiplied Sy by -2 resulting in the expression-10y - 3. He should have only multiplied 3 by -2 and subtracted

Step-by-step answer

P Answered by PhD

the answer is B. He should have only multiplied 3 by –2 resulting in the expression 5y – 6.

Step-by-step explanation:

Physics

On a one lane road, a person driving a car at v1 = 54 mi/h suddenly notices a truck 2.4 mi in front of him. That truck is moving in the same direction at v2 = 31 mi/h. In order to avoid a collision, the person has to reduce the speed of his car to v2 during time interval Δt. The smallest magnitude of acceleration required for the car to avoid a collision is a. During this problem, assume the direction of motion of the car is the positive direction. ( I need help with b,e,g,h,i.) (a) Enter an expression, in terms of defined quantites, for the distance

Step-by-step answer

P Answered by PhD

1

a) Δx₂ = 31*Δt

b) Δx₁ = 977.5 / a

c) a = 23 / Δt

e) Δx₁ = 42.5*Δt

g) Δt = 0.0565 h

i) a = 0.05 m/s²

Explanation:

Given

v₁ = 54 Mi/h

v₂ = 31 Mi/h

a) We apply the formula

Δx₂ = v₂*Δt

⇒ Δx₂ = 31*Δt (Assuming constant speed)

b) We use the formula

v₂² = v₁² - 2*a*Δx₁ ⇒ Δx₁ = (v₁² - v₂²) / (2*a)

⇒ Δx₁ = (54² - 31²) / (2*a)

⇒ Δx₁ = 977.5 / a

c) We use the equation

v₂ = v₁ - a*Δt ⇒ a = (v₁ - v₂) / Δt

⇒ a = (54 - 31) / Δt

⇒ a = 23 / Δt

e) We apply the formula

Δx₁ = v₁*Δt - 0.5*a*Δt²

Δx₁ = 54*Δt - 0.5*(23 / Δt)*Δt²

⇒ Δx₁ = 42.5*Δt

g) If Δx₁ = 2.4 Mi ⇒ 2.4 = 42.5*Δt ⇒ Δt = 0.0565 h

i) If a = 23 / Δt ⇒ a = 23 Mi / 0.0565 h = 407.29 Mi/h²

⇒ a = 0.05 m/s²

Mathematics

John claims the following two expressions are equivalent. - 215y - 3) = - 10y - 6 John s work in determining an expression equivalent to the first expression is shown below. - 2/5y - 3) = (-2x5y) - (-2x - 3) = - 10y-6 Which statement explains why John s claim is incorrect? He should have subtracted (-2 * 3) resulting in the expression–10y + 6. He should have only multiplied 3 by -2 resulting in the expression 5y - 6. He should have only multiplied Sy by -2 resulting in the expression-10y - 3. He should have only multiplied 3 by -2 and subtracted

Step-by-step answer

P Answered by PhD

the answer is B. He should have only multiplied 3 by –2 resulting in the expression 5y – 6.

Step-by-step explanation:

Physics

On a one lane road, a person driving a car at v1 = 54 mi/h suddenly notices a truck 2.4 mi in front of him. That truck is moving in the same direction at v2 = 31 mi/h. In order to avoid a collision, the person has to reduce the speed of his car to v2 during time interval Δt. The smallest magnitude of acceleration required for the car to avoid a collision is a. During this problem, assume the direction of motion of the car is the positive direction. ( I need help with b,e,g,h,i.) (a) Enter an expression, in terms of defined quantites, for the distance

Step-by-step answer

P Answered by PhD

1

a) Δx₂ = 31*Δt

b) Δx₁ = 977.5 / a

c) a = 23 / Δt

e) Δx₁ = 42.5*Δt

g) Δt = 0.0565 h

i) a = 0.05 m/s²

Explanation:

Given

v₁ = 54 Mi/h

v₂ = 31 Mi/h

a) We apply the formula

Δx₂ = v₂*Δt

⇒ Δx₂ = 31*Δt (Assuming constant speed)

b) We use the formula

v₂² = v₁² - 2*a*Δx₁ ⇒ Δx₁ = (v₁² - v₂²) / (2*a)

⇒ Δx₁ = (54² - 31²) / (2*a)

⇒ Δx₁ = 977.5 / a

c) We use the equation

v₂ = v₁ - a*Δt ⇒ a = (v₁ - v₂) / Δt

⇒ a = (54 - 31) / Δt

⇒ a = 23 / Δt

e) We apply the formula

Δx₁ = v₁*Δt - 0.5*a*Δt²

Δx₁ = 54*Δt - 0.5*(23 / Δt)*Δt²

⇒ Δx₁ = 42.5*Δt

g) If Δx₁ = 2.4 Mi ⇒ 2.4 = 42.5*Δt ⇒ Δt = 0.0565 h

i) If a = 23 / Δt ⇒ a = 23 Mi / 0.0565 h = 407.29 Mi/h²

⇒ a = 0.05 m/s²

Computers and Technology

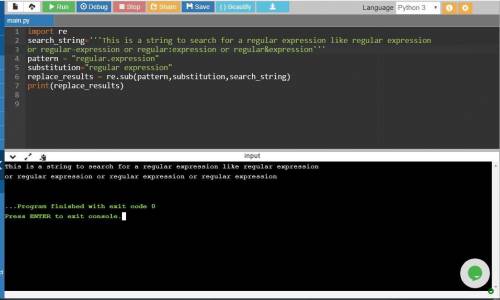
Regular Expression Replace Challenge In this challenge you will use the file regex_replace_challenge_student.py to: Write a regular expression that will replace all occurrences of: regular-expression regular:expression r egular&expression In the string: This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression Assign the regular expression to a variable named pattern Using the sub() method from the re package substitute all occurrences of the pattern with

Step-by-step answer

P Answered by Master

Here is the Python program:

import re # module for regular expressions

search_string='''This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression''' #string to search for a regular expression

pattern = "regular.expression" #Assigns the regular expression to pattern

substitution="regular expression" #substitute all occurrences of pattern with regular expression string stored in substitution

replace_results = re.sub(pattern,substitution,search_string) # sub() method from the re package to substitute all occurrences of the pattern with substitution

print(replace_results) #Assigns the outcome of the sub() method to this variable

Explanation:

This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression

search_string='''This is a string to search for a regular expression like regular expression or regular-expression or regular:expression or regular&expression'''

The following statement assigns the regular expression to a variable named pattern .

pattern = "regular.expression"

The following statement is used to substitute the pattern (regular expression) in the search_string by replacing all occurrences of "regular expression" sub-string on search_string.

substitution="regular expression"

The following statement uses re.sub() method to replace all the occurrences of a pattern with another sub string ("regular expression"). This means in search_string, the sub strings like regular expression, regular-expression, regular:expression or regular&expression are replaced with string "regular expression". This result is stored in replace_results variable. Three arguments are passed to re.sub() method:

sub string to replace i.e. pattern

sub string to replace with i.e. substitution

The actual string i.e. search_string

replace_results = re.sub(pattern,substitution,search_string)

The following print statement displays the output of replace_results

print(replace_results)

The output of the above program is:

This is a string to search for a regular expression like regular expression or regular expression or regular expression or regular expression

Regular Expression Replace Challenge

In this challenge you will use the file regex_replace_challeng

Mathematics

The volume (in cubic meters), v, of a rectangular room is given by the expression: v = 7b^4-28 where b is a positive integer and each dimension is a positive integer too. what are three unique expressions that could represent the dimensions of the room? write these three expressions as a product that equals the volume (e.g. (expression 1)(expression 2)(expression 3) ).

Step-by-step answer

P Answered by PhD

1

7(b^2 -2)(b^2 +2)

Step-by-step explanation:

Factoring the common factor 7 from both terms, you get the difference of squares. That can also be factored.

v = 7(b^4 -4) = 7(b^2 -2)(b^2 +2)

The difference b^2-2 will have irrational factors, so does not meet the problem requirements. This is the factorization over integers.

Mathematics

Can someone just answer this asap for ’ the volume (in cubic meters), v, of a rectangular room is given by the expression: v = 162 - 2b^6 where b is a positive integer and each dimension is an integer greater than 1 meter. what are three unique expressions that could represent the dimensions of the room in terms of b? write these three expressions as a product that equals the volume (e.g. (expression 1)(expression 2)(expression 3) ).

Step-by-step answer

P Answered by PhD

2

ANSWER

The three expressions are

$V = 2(9 - {b}^{3} )(9 + {b}^{3} )$

EXPLANATION

We were given the volume in cubic units to

$V = 162 - 2 {b}^{6}$

If we factor 2, we get,

$V = 2(81 - {b}^{6} )$

The expression in parenthesis is a difference of two squares. But you may not recognize it at first sight.

$V = 2( {9}^{2} - ({b}^{3})^{2} )$

This further gives us.

$V = (2)(9 - {b}^{3} )(9 + {b}^{3} )$

Mathematics

Can someone just answer this asap for ’ the volume (in cubic meters), v, of a rectangular room is given by the expression: v = 162 - 2b^6 where b is a positive integer and each dimension is an integer greater than 1 meter. what are three unique expressions that could represent the dimensions of the room in terms of b? write these three expressions as a product that equals the volume (e.g. (expression 1)(expression 2)(expression 3) ).

Step-by-step answer

P Answered by PhD

2

ANSWER

The three expressions are

$V = 2(9 - {b}^{3} )(9 + {b}^{3} )$

EXPLANATION

We were given the volume in cubic units to

$V = 162 - 2 {b}^{6}$

If we factor 2, we get,

$V = 2(81 - {b}^{6} )$

The expression in parenthesis is a difference of two squares. But you may not recognize it at first sight.

$V = 2( {9}^{2} - ({b}^{3})^{2} )$

This further gives us.

$V = (2)(9 - {b}^{3} )(9 + {b}^{3} )$

Which expression can be used to find AC

Step-by-step answer

Faq

Try asking the Studen AI a question.