solve the system using elimination. show all, №18011229, 20.08.2020 15:09

Mathematics

PLEASE HURRY Solve each system by elimination. Show your work. Write out answers as ordered pairs. 3) 4x + y = -18 and 2x + 4y = -16

Step-by-step answer

P Answered by Master

2

Step-by-step explanation:

4x+y=-18

4x+8y=-32

Subtracting the equations we get

-7y = 14

y=-2

4x+(-2)=-18

4x = -18+2

4x=-16

x=-4

Mathematics

solve the system using elimination. show all work. write your answer in the form (x,y) 2x-3y=18 x+y=14

Step-by-step answer

P Answered by Specialist

x=12 y=2

Step-by-step explanation:

Due to fractions have screen shorted the steps in the image above

solve the system using elimination. show all work. write your answer in the form (x,y) 2x-3y=18 x+y=

Mathematics

PLEASE HURRY Solve each system by elimination. Show your work. Write out answers as ordered pairs. 3) 4x + y = -18 and 2x + 4y = -16

Step-by-step answer

P Answered by Specialist

2

Step-by-step explanation:

4x+y=-18

4x+8y=-32

Subtracting the equations we get

-7y = 14

y=-2

4x+(-2)=-18

4x = -18+2

4x=-16

x=-4

Mathematics

Perform an operation on the given system that eliminates the indicated variable. write the new equivalent system. 2x + y − 4z = 4, 2x + 4y + z = 15, 6x − 5y − z = 7 eliminate the x-term from the third equation.

Step-by-step answer

P Answered by PhD

8y-11z=5

Step-by-step explanation:

2x + y − 4z = 4, A

2x + 4y + z = 15,B

6x − 5y − z = 7C

Solving A to find the value of x

2x= 4-y+4z

x=4-y+4z/2D

Putting D in C

6(4-y+4z/2) -5y -z=7

3(4-y+4z) -5y-z=7

12-3y+12z-5y-z=7

12-8y + 11z=7

-8y +11z= 7-12

-8y +11z= -5

8y-11z=5E

Mathematics

Iwill give you the brainlessest if you awnser the following plz and you so much 2. the sum of two numbers is 82. their difference is 24. write a system of equations that describes this situation. solve by elimination to find the two numbers. 3. solve the system of equations using substitution. y = 4x + 6 y = 2x 4.solve the system using elimination. 5x + 8y = –29 7x – 2y = –67 5. what is the solution of the system of equations? y = –4x + 6 y = –5x – 4 6.suppose you are determining the growth rate of two species of plants. species a is 12 cm tall

Step-by-step answer

P Answered by PhD

32

2. x + y = 82
x - y = 24
add
2x = 106
x = 53

x + y = 82
53 + y = 82
y = 82 - 53
y = 29

solution is : (53,29)

3. y = 2x
y = 4x + 6

2x = 4x + 6
2x - 4x = 6
-2x = 6
x = -3

y = 2x
y = 2(-3)
y = -6

solution is (-3,-6)

4. 5x + 8y = -29
7x - 2y = -67...multiply by 4

5x + 8y = -29
28x - 8y = - 268 ..result of multiplying by 4
add
33x = - 297
x = - 9

5x + 8y = -29
5(-9) + 8y = -29
-45 + 8y = -29
8y = -29 + 45
8y = 16
y = 2

solution is : (-9,2)

5. y = -4x + 6
y = -5x - 4

-4x + 6 = -5x - 4
-4x + 5x = -4 - 6
x = -10

y = -4x + 6
y = -4(-10) + 6
y = 40 + 6
y = 46

solution is (-10,46)

6. H(m) = 2m + 12
H(m) = 3m + 10

7. -8x + 4y > -52
4y > 8x - 52
y > 2x - 13 <==

8. 3x - y = 28
3x + y = 14
add
6x = 42
x = 7

3x - y = 28
3(7) - y = 28
21 - y = 28
-y = 28 - 21
-y = 7
y = -7

solution is (7,-7)

10. 5x - 5y > 70
-5y > -5x + 70
y < x - 14 <==

11. sorry...dont know

12. y = 4x + 4
y = -3x - 3

4x + 4 = -3x - 3
4x + 3x = -3 - 4
7x = -7
x = -1

y = 4x + 4
y = 4(-1) + 4
y = 0

solution is (-1,0)

13. -12x - 2y > - 42
-2y > 12x - 42
y < -6x + 21 <==

14. -5x + 2y = 9
3x + 5y = 7

solution is (-1,2)

15. 3x + 6y = -2
15x + 30y = -10divide by 5 to reduce = 3x + 6y = -2
is the same lineinfinite solutions

1. (the graph)y < = 3x - 43rd one

9. (2nd graph)y < = -3x + 4last one

Mathematics

Iwill give you the brainlessest if you awnser the following plz and you so much 2. the sum of two numbers is 82. their difference is 24. write a system of equations that describes this situation. solve by elimination to find the two numbers. 3. solve the system of equations using substitution. y = 4x + 6 y = 2x 4.solve the system using elimination. 5x + 8y = –29 7x – 2y = –67 5. what is the solution of the system of equations? y = –4x + 6 y = –5x – 4 6.suppose you are determining the growth rate of two species of plants. species a is 12 cm tall

Step-by-step answer

P Answered by PhD

32

2. x + y = 82
x - y = 24
add
2x = 106
x = 53

x + y = 82
53 + y = 82
y = 82 - 53
y = 29

solution is : (53,29)

3. y = 2x
y = 4x + 6

2x = 4x + 6
2x - 4x = 6
-2x = 6
x = -3

y = 2x
y = 2(-3)
y = -6

solution is (-3,-6)

4. 5x + 8y = -29
7x - 2y = -67...multiply by 4

5x + 8y = -29
28x - 8y = - 268 ..result of multiplying by 4
add
33x = - 297
x = - 9

5x + 8y = -29
5(-9) + 8y = -29
-45 + 8y = -29
8y = -29 + 45
8y = 16
y = 2

solution is : (-9,2)

5. y = -4x + 6
y = -5x - 4

-4x + 6 = -5x - 4
-4x + 5x = -4 - 6
x = -10

y = -4x + 6
y = -4(-10) + 6
y = 40 + 6
y = 46

solution is (-10,46)

6. H(m) = 2m + 12
H(m) = 3m + 10

7. -8x + 4y > -52
4y > 8x - 52
y > 2x - 13 <==

8. 3x - y = 28
3x + y = 14
add
6x = 42
x = 7

3x - y = 28
3(7) - y = 28
21 - y = 28
-y = 28 - 21
-y = 7
y = -7

solution is (7,-7)

10. 5x - 5y > 70
-5y > -5x + 70
y < x - 14 <==

11. sorry...dont know

12. y = 4x + 4
y = -3x - 3

4x + 4 = -3x - 3
4x + 3x = -3 - 4
7x = -7
x = -1

y = 4x + 4
y = 4(-1) + 4
y = 0

solution is (-1,0)

13. -12x - 2y > - 42
-2y > 12x - 42
y < -6x + 21 <==

14. -5x + 2y = 9
3x + 5y = 7

solution is (-1,2)

15. 3x + 6y = -2
15x + 30y = -10divide by 5 to reduce = 3x + 6y = -2
is the same lineinfinite solutions

1. (the graph)y < = 3x - 43rd one

9. (2nd graph)y < = -3x + 4last one

Mathematics

1. solve the system using elimination -4x + 4y = -8 x = 4y = -7 2. what is the solution of the system? write answer in (x,y) form. -8x + 2y = -26 -5x - 5y = -10 3. solve the system using an equivalent system. 3x - 5y = 9 3x - y = -3 4. what are the solutions of the following systems? -x + y = -2 4x - 4y = 8

Step-by-step answer

P Answered by Specialist

1

1. (7.4,3.6)

2. (3,-1)

3. (-2,-3)

4. Infinite number of solutions.

Step-by-step explanation:

We can solve systems of equations 3 ways: graphing, substitution, and elimination. We will solve 1-2, 4 using substitution and 3 with elimination.

1. Since x=4y-7, we substitute it in for x . It's better than elimination because of how it is set-up unless there is a typo.

So -4x+4y=-8 becomes -4(4y-7)+4y=-8. We simplify to -14y+28+4y=-8. We add like terms to get -10y+28=-8. We now solve for y by subtracting 28 and dividing by -10.-10y+28-28=-8-28-10y=-36y=3.6We substitute y=3.6 into x=4y-7. x=4(3.6)-7=14.4-7=7.4

2. Since none of the coefficients of x & y are the same, we will rearrange and substitute.

-8x+2y=-26 becomes 2y=8x-26 by adding 8x to both side.We divide by 2. y=4x-13.We substitute into -5x-5y=-10. -5x-5(4x-13)=-10We simplify to -5x-20x+65=-10We add like terms. -25x+65=-10We now solve for x by subtracting 65 and dividing by -25.-25x+65-65=-10-65-25x=-75x=3We substitute x=3 into -8(3)+2y=-26-24+2y=-262y=-2y=-1

3. We can solve this system through elimination. We subtract or add the equations when the coefficients are the same to eliminate one variable.

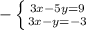
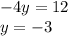
$-\left \{ {{3x-5y=9} \atop {3x-y=-3}} \right.$ $-4y=12\\y=-3$ We susbstitute y=-3 into one of the equations 3x-(-3)=-3.3x=-6x=-2

4. Since none of the coefficients of x & y are the same, we will rearrange and substitute.

-x+y=-2 becomes y=x-2We substitute into 4x-4(x-2)=8.Simplify 4x-4x+8=8.Add like terms 0x+8=88=8This is a true statement and a special solution. It means infinite number of solutions.