I need help figuring out the answers for this

1. For this problem we just refer to the descriptions that you placed under the prompt. According to Malcolm's bandmate, it would be easier to solve the trinomial by subtracting 350 from both sides and then factoring the equation. Malcolm, on the other hand, thinks that we should manipulate the equation in order to make it a perfect square trinomial.

2. This trinomial would be easily solved by using Malcolm's idea. As Malcolm pointed out, you just need to apply a formula to manipulate the equation then you can find the roots in no time. Finding the factors of 350 just to solve the trinomial would be the hard way to go since you would be considering a lot of them.

3. For this item, we are just tasked to follow what Malcolm's bandmate started doing. So, we would just need to think of two numbers that would result to -350 when multiplied. To start off, let's think of something we can divide 350 by, let's say 70. Now, if we divide -350 by 70 the result would be -5 therefore that would be our two numbers (p and q). p + q would therefore just be 65.

p = 70
q = -5
p + q = 65

4. No, the factor table is not complete since you would need factors of -350 that would add up to -3, the coefficient of w. This rule is sort of a shortcut when factoring the trinomial, since expressing the roots in the form of (w + p)(w + q) would lead you to the original expression by following the rules. We do not see any factors that add up to -3 in the factor table.

5. Malcolm was almost right, but technically he missed the initial step. To make a perfect square trinomial, you first need to make sure that a (or the coefficient of the leading term) is equal to one. If not, you first need to divide the entire equation by a. Then, you apply what Malcolm says.

6. Since the coefficient of the leading term is already equal to one, we do not need to worry about the initial step anymore. For this item, we just need to divide -3 by two and square it then add the resulting number to both sides. The solution is shown below:





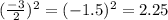
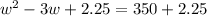
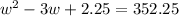
7. To factor the trinomial, we just really need to make sense of the process we just did in the previous item. Notice that we just squared -1.5, after dividing -3 by 2. If you look at it closely, this is just the process of expanding the square of a binomial in reverse. Therefore, we know that our resulting expression is the square of (w - 1.5)



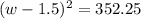
8. For this item we are just simply tasked to follow the instructions given. The process described in the item is how we are supposed to solve for the variable. The work and solution for this item is shown below:





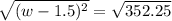
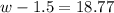
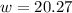
9. The solution does make sense in terms of the problem because, firstly, the answer we have arrived on is a positive number which means it is a realistic value of a measurement, and secondly, our solution in the previous item just followed basic arithmetic so we did not violate anything in the problem.

10. For this item, we can find the length by subtracting the value of the width by 3, as was dictated in the prompt. But before this, we first need to round our answer for the width to the nearest foot. 20 minus 3 is just 17. Multiplying 20 and 17 might not get us to 350 but this is just an approximation anyway. (Getting the product of the numbers before rounding off would give us an accurate one.)

w = 20 feet
l = 17 feet

I believe the answer is: C figuring out the price per unit and comparing it to other choices

Price comparison is used as one of the basis to make purchase decision by the consumers in the market. The purpose of price comparison is to determine whether the price of a certain product is appropriate compared to the value that they can give after considering other alternatives.

I believe the answer is: C figuring out the price per unit and comparing it to other choices

Price comparison is used as one of the basis to make purchase decision by the consumers in the market. The purpose of price comparison is to determine whether the price of a certain product is appropriate compared to the value that they can give after considering other alternatives.

A, context clues allow us to identify the meaning of a word through identification of words that may help us understand the meaning through implied definitions

The correct answer is D. Doubling a recipe and figuring out how many cans of paint to use are both examples of using math skills.

In option A, it states that neither doubling a recipe nor figuring out how many cans of paint to use is an example of using math skills. However, this is not correct. Doubling a recipe involves multiplying the ingredients by 2, which requires basic multiplication skills. Figuring out how many cans of paint to use also involves calculations, such as measuring the area to be painted and determining the coverage of each can of paint.

Option B states that Michael doubled a recipe and made delicious chocolate-chip cookies. This example reinforces the fact that he used math skills by doubling the quantities of the ingredients.

Option C states that Michael figured out how many cans of paint to buy to repaint his room. This also requires math skills as he would need to calculate the area of the room, consider the coverage of the paint, and determine the number of cans required for adequate coverage.

Therefore, both doubling a recipe and figuring out how many cans of paint to use involve applying math skills, making option D the correct answer.